CF1498C Planar Reflections

Gaurang 生活在一个神秘的宇宙中。他面对着 $n$ 个连续的二维平面。他向这些平面发射了一个衰变年龄为 $k$ 的粒子。 粒子可以直接穿过一个平面，然而，每个平面都会产生一个完全相同的粒子副本，该副本朝相反方向运动且衰变年龄为 $k-1$。如果粒子的衰变年龄等于 $1$，则不会产生副本。 例如，如果有两个平面，且发射了一个衰变年龄为 $3$ 的粒子（向右运动），过程如下（这里 $D(x)$ 表示一个衰变年龄为 $x$ 的粒子）： 1. 第一个平面产生一个向左的 $D(2)$，并让 $D(3)$ 继续向右运动； 2. 第二个平面产生一个向左的 $D(2)$，并让 $D(3)$ 继续向右运动； 3. 第一个平面让 $D(2)$ 继续向左运动，并产生一个向右的 $D(1)$； 4. 第二个平面让 $D(1)$ 继续向右运动（$D(1)$ 不会产生任何副本）。 最终，粒子的多重集 $S$ 为 $\{D(3), D(2), D(2), D(1)\}$。（参见注释中的测试案例图示说明。） 当平面数量过大时，Gaurang 无法应对这种复杂情况。请帮助 Gaurang 在给定 $n$ 和 $k$ 的情况下，计算多重集 $S$ 的大小。 由于多重集的大小可能非常大，你需要输出其对 $10^9+7$ 取模的结果。 注意：粒子可以在平面之间来回运动而不会相互碰撞。

输入的第一行包含测试用例的数量 $t$（$1 \le t \le 100$）。随后 $t$ 行，每行包含两个整数 $n$ 和 $k$（$1 \le n, k \le 1000$）。 此外，所有测试用例的 $n$ 之和不超过 $1000$，所有测试用例的 $k$ 之和不超过 $1000$。同一测试中的所有测试用例均不同。

输出 $t$ 个整数。第 $i$ 个整数应为第 $i$ 个测试用例的答案。

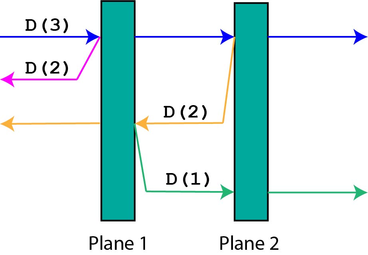
让我们解释第一个样例中的四个测试用例。 测试用例 1：（$n = 2$，$k = 3$）已在题目描述中解释。 参见下图模拟过程。每条不同颜色的直线代表不同粒子的路径。可以看到，多重集中共有四个不同的粒子。注意，反射粒子之间的垂直间距仅用于视觉清晰（如前所述，任何两个不同的粒子都不会相互碰撞）。  测试用例 2：（$n = 2$，$k = 2$）解释如下： 1. 第一个平面产生一个向左的 $D(1)$，并让 $D(2)$ 继续向右运动； 2. 第二个平面产生一个向左的 $D(1)$，并让 $D(2)$ 继续向右运动； 3. 第一个平面让 $D(1)$ 继续向左运动（$D(1)$ 不会产生任何副本）。 最终的多重集 $\{D(1), D(1), D(2)\}$ 的大小为三。 测试用例 3：（$n = 3$，$k = 1$），有三个平面，但衰变年龄仅为 $1$。因此粒子穿过平面时不会产生新副本。因此，答案为 $1$。 测试用例 4：（$n = 1$，$k = 3$）只有一个平面。粒子产生一个向左的新副本。多重集 $\{D(2), D(3)\}$ 的大小为 $2$。 翻译由 DeepSeek V3 完成