CF1499F Diameter Cuts

给定一个整数 $k$ 和一棵包含 $n$ 个顶点的无向树。 一条简单路径（即每个顶点最多出现一次的路径）在某对顶点之间的长度定义为该路径上的边数。树的直径是所有顶点对之间简单路径的最大长度。 你需要从树中移除一些边。移除这些边后，树会被分割成若干棵更小的树。如果所有分割出来的树的直径都不超过 $k$，那么这组被移除的边就是合法的。 如果存在某条边只出现在其中一个集合中，则两组边集被认为是不同的。 请你计算合法的边集数量，对 $998\,244\,353$ 取模。

第一行包含两个整数 $n$ 和 $k$（$2 \le n \le 5000$，$0 \le k \le n - 1$），分别表示树的顶点数和允许的最大直径。 接下来的 $n-1$ 行，每行包含两个整数 $v$ 和 $u$（$1 \le v, u \le n$，$v \neq u$），表示树中的一条边。 给定的边保证构成一棵树。

输出一个整数，表示合法的边集数量，对 $998\,244\,353$ 取模。

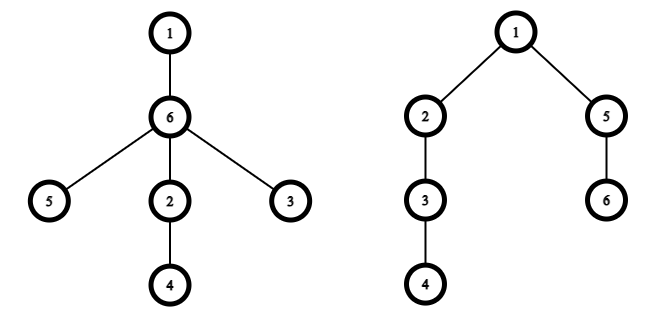
在第一个样例中，给定树的直径已经不超过 $k$。因此，你可以选择移除任意集合的边，分割出来的所有树的直径都不超过 $k$。一共有 $2^3$ 种选择，包括不移除任何边。 在第二个样例中，你必须移除唯一的一条边。否则，直径为 $1$，大于 $0$。 下面是第三个和第四个样例的树结构：  由 ChatGPT 4.1 翻译