CF1503E 2-Coloring

有一个 $n$ 行 $m$ 列的网格。网格中的每个格子都要被涂成蓝色或黄色。 如果一个网格的涂色满足以下条件，则称其为“愚蠢的涂色”：每一行恰好有一段连续的蓝色格子，每一列恰好有一段连续的黄色格子。 换句话说，每一行必须至少有一个蓝色格子，且该行所有蓝色格子必须连续；同样地，每一列必须至少有一个黄色格子，且该列所有黄色格子必须连续。 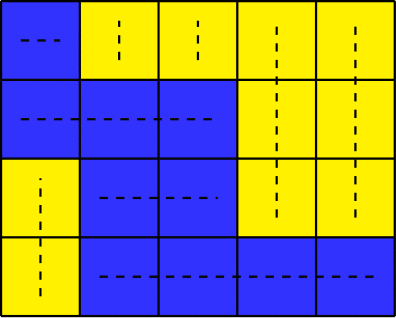 这是一个“愚蠢的涂色”的例子。 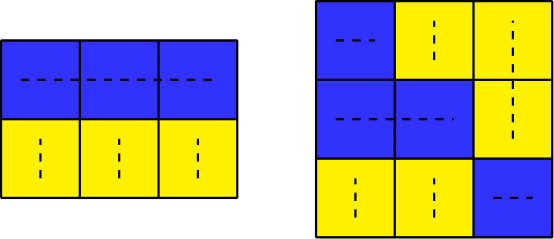 这些是“聪明的涂色”的例子。第一个涂色在第二行缺少蓝色格子，第二个涂色在第二列有两段黄色格子。 问有多少种不同的“愚蠢的涂色”方案？如果存在某个格子的颜色不同，则认为两种涂色方案不同。

一行包含两个整数 $n$ 和 $m$，表示网格的行数和列数，$1\le n, m\le 2021$。

输出一个整数，表示“愚蠢的涂色”方案数，对 $998244353$ 取模。

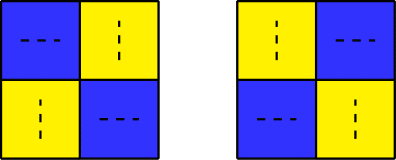
在第一个测试用例中，只有如下两种 $2\times 2$ 的“愚蠢的涂色”方案。  由 ChatGPT 4.1 翻译