CF1508C Complete the MST

作为一名教师，Riko Hakozaki 经常需要帮助她的学生解决各类学科的问题。今天，她被问到了一个编程任务，内容如下： 给定一个无向完全图，包含 $n$ 个节点，其中部分边已经被赋予了正权值，其余边尚未赋值。你需要为所有未赋值的边分配非负权值，使得最终所有边都被赋值后的完全图中，所有边权的异或和等于 $0$。 定义一个完全赋值的完全图的“丑陋度”为其最小生成树的权值，即最小生成树所有边权之和。你需要合理分配权值，使得最终图的丑陋度尽可能小。 提示：一个无向完全图有 $n$ 个节点，包含所有 $1 \le u < v \le n$ 的边；这样的图共有 $\frac{n(n-1)}{2}$ 条边。 她不确定如何解决这个问题，因此请你帮她解决。

第一行包含两个整数 $n$ 和 $m$（$2 \le n \le 2 \cdot 10^5$，$0 \le m \le \min(2 \cdot 10^5, \frac{n(n-1)}{2} - 1)$）——节点数和已赋权边的数量。保证至少有一条边未赋值。 接下来的 $m$ 行，每行包含三个整数 $u_i$、$v_i$ 和 $w_i$（$1 \le u_i, v_i \le n$，$u \ne v$，$1 \le w_i < 2^{30}$），表示从 $u_i$ 到 $v_i$ 的边已被赋予权值 $w_i$。输入中不会有重复的边。

输出一行一个整数，表示所有权值分配方案中，异或和为 $0$ 时的最小丑陋度。

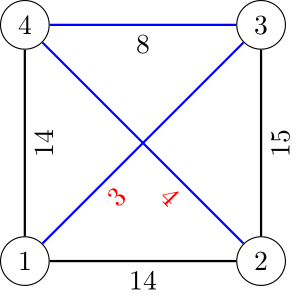
下图展示了第一个测试用例。黑色权值为题目中已赋值的边，红色权值为我们分配的边，蓝色边为最小生成树。  由 ChatGPT 4.1 翻译