CF1508C Complete the MST

As a teacher, Riko Hakozaki often needs to help her students with problems from various subjects. Today, she is asked a programming task which goes as follows. You are given an undirected complete graph with $ n $ nodes, where some edges are pre-assigned with a positive weight while the rest aren't. You need to assign all unassigned edges with non-negative weights so that in the resulting fully-assigned complete graph the [XOR](https://en.wikipedia.org/wiki/Bitwise_operation#XOR) sum of all weights would be equal to $ 0 $ . Define the ugliness of a fully-assigned complete graph the weight of its [minimum spanning tree](https://en.wikipedia.org/wiki/Minimum_spanning_tree), where the weight of a spanning tree equals the sum of weights of its edges. You need to assign the weights so that the ugliness of the resulting graph is as small as possible. As a reminder, an undirected complete graph with $ n $ nodes contains all edges $ (u, v) $ with $ 1 \le u < v \le n $ ; such a graph has $ \frac{n(n-1)}{2} $ edges. She is not sure how to solve this problem, so she asks you to solve it for her.

The first line contains two integers $ n $ and $ m $ ( $ 2 \le n \le 2 \cdot 10^5 $ , $ 0 \le m \le \min(2 \cdot 10^5, \frac{n(n-1)}{2} - 1) $ ) — the number of nodes and the number of pre-assigned edges. The inputs are given so that there is at least one unassigned edge. The $ i $ -th of the following $ m $ lines contains three integers $ u_i $ , $ v_i $ , and $ w_i $ ( $ 1 \le u_i, v_i \le n $ , $ u \ne v $ , $ 1 \le w_i < 2^{30} $ ), representing the edge from $ u_i $ to $ v_i $ has been pre-assigned with the weight $ w_i $ . No edge appears in the input more than once.

Print on one line one integer — the minimum ugliness among all weight assignments with XOR sum equal to $ 0 $ .

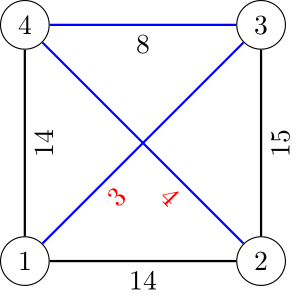
The following image showcases the first test case. The black weights are pre-assigned from the statement, the red weights are assigned by us, and the minimum spanning tree is denoted by the blue edges.