CF1508D Swap Pass

基于篮球训练中的一个奇特事件，Akari 想出了如下的竞赛编程问题！ 给定平面上的 $n$ 个点，保证任意三点不共线。第 $i$ 个点初始有一个标签 $a_i$，其中 $a_1, a_2, \dots, a_n$ 构成 $1, 2, \dots, n$ 的一个排列。 你可以通过以下操作修改标签： 1. 选择两个不同的整数 $i$ 和 $j$，其中 $1 \le i, j \le n$。 2. 交换第 $i$ 个点和第 $j$ 个点的标签，最后 3. 画出连接第 $i$ 个点和第 $j$ 个点的线段。 如果一系列操作满足：按顺序执行所有操作后，第 $k$ 个点的标签为 $k$（$1 \le k \le n$），且所有画出的线段两两内部不相交（即如果两条线段相交，则它们必须在两条线段的公共端点处相交），则称该操作序列是合法的。 特别地，所有画出的线段必须互不相同。 请你找出任意一个合法的操作序列，或者说明不存在这样的序列。

第一行包含一个整数 $n$（$3 \le n \le 2000$），表示点的数量。 接下来的 $n$ 行，每行包含三个整数 $x_i$、$y_i$、$a_i$（$-10^6 \le x_i, y_i \le 10^6$，$1 \le a_i \le n$），表示第 $i$ 个点的坐标为 $(x_i, y_i)$，初始标签为 $a_i$。 保证所有点互不相同，任意三点不共线，且 $a_1, a_2, \dots, a_n$ 构成 $1, 2, \dots, n$ 的一个排列。

如果不存在合法的操作序列，输出 $-1$。 否则，输出一个整数 $k$（$0 \le k \le \frac{n(n-1)}{2}$），表示操作次数。接下来 $k$ 行，每行包含两个整数 $i$ 和 $j$（$1 \le i, j \le n$，$i \neq j$），表示本次操作选择的两个点的编号。 注意，你不需要使 $k$ 最小或最大。 如果有多组答案，输出任意一组均可。

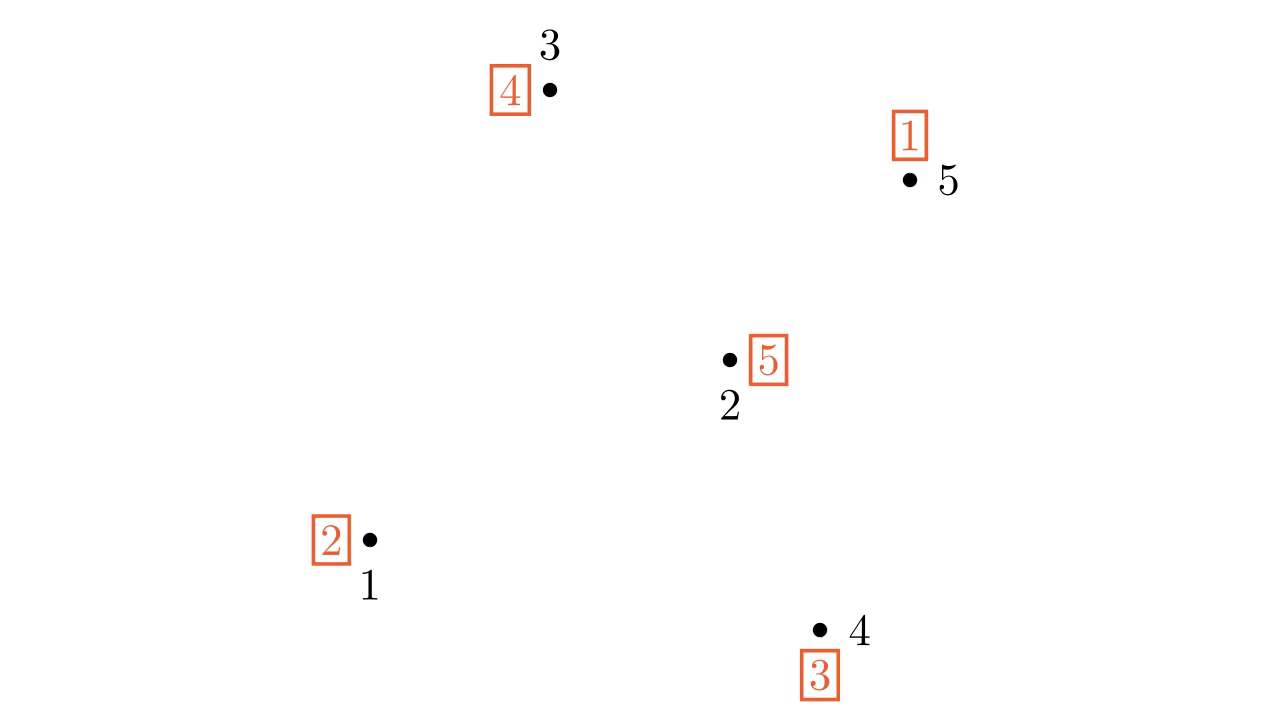
下图展示了第一个样例测试的动画。黑色数字表示点的编号，橙色方框内的数字表示它们的标签。  在第二个测试用例中，所有标签已经在正确的位置，因此不需要任何操作。 由 ChatGPT 4.1 翻译