CF1508F Optimal Encoding

Touko 最喜欢的数列是 $a_1, a_2, \dots, a_n$，它是 $1, 2, \dots, n$ 的一个排列。她希望找到一些与她最喜欢的排列相似的排列集合。 她有 $q$ 个区间 $[l_i, r_i]$，其中 $1 \le l_i \le r_i \le n$。为了构造与她最喜欢的排列相似的排列，她给出了如下定义： - 如果排列 $b_1, b_2, \dots, b_n$ 允许区间 $[l', r']$ 保持其形状，则对于任意整数对 $(x, y)$，满足 $l' \le x < y \le r'$，有 $b_x < b_y$ 当且仅当 $a_x < a_y$。 - 如果排列 $b_1, b_2, \dots, b_n$ 允许所有 $1 \le i \le k$ 的区间 $[l_i, r_i]$ 保持其形状，则称 $b$ 是 $k$-相似的。 Yuu 想为 Touko 找出所有 $k$-相似的排列，但这是一项非常困难的任务；于是，Yuu 决定用有向无环图（DAG）来编码所有 $k$-相似的排列集合。Yuu 还为自己定义了如下概念： - 如果排列 $b_1, b_2, \dots, b_n$ 满足 DAG $G'$，则对于 $G'$ 中的每一条边 $u \to v$，都必须有 $b_u < b_v$。 - $k$-编码是一个以 $1, 2, \dots, n$ 为顶点的 DAG $G_k$，使得排列 $b_1, b_2, \dots, b_n$ 满足 $G_k$ 当且仅当 $b$ 是 $k$-相似的。 由于 Yuu 今天很空，她想要计算出对于每个 $k$ 从 $1$ 到 $q$，所有 $k$-编码中最少的边数。

第一行包含两个整数 $n$ 和 $q$（$1 \le n \le 25\,000$，$1 \le q \le 100\,000$）。 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$，它们是 $1, 2, \dots, n$ 的一个排列。 接下来的 $q$ 行，每行包含两个整数 $l_i$ 和 $r_i$（$1 \le l_i \le r_i \le n$）。

输出 $q$ 行。第 $k$ 行输出一个整数，表示所有 $k$-编码中最少的边数。

对于第一个测试用例： - 所有 $1$-相似的排列必须允许区间 $[1, 3]$ 保持其形状。因此，所有 $1$-相似的排列为 $\{[3, 4, 2, 1], [3, 4, 1, 2], [2, 4, 1, 3], [2, 3, 1, 4]\}$。这些排列的最优编码如下图所示： - 所有 $2$-相似的排列必须允许区间 $[1, 3]$ 和 $[2, 4]$ 保持其形状。因此，所有 $2$-相似的排列为 $\{[3, 4, 1, 2], [2, 4, 1, 3]\}$。这些排列的最优编码如下图所示： - 所有 $3$-相似的排列必须允许区间 $[1, 3]$、$[2, 4]$ 和 $[1, 4]$ 保持其形状。因此，所有 $3$-相似的排列仅包含 $[2, 4, 1, 3]$。该排列的最优编码如下图所示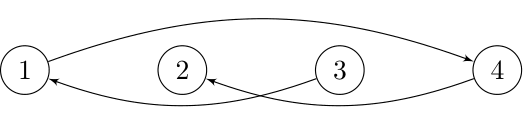： 由 ChatGPT 4.1 翻译