CF150C Smart Cheater
Description
I guess there's not much point in reminding you that Nvodsk winters aren't exactly hot. That increased the popularity of the public transport dramatically. The route of bus $ 62 $ has exactly $ n $ stops (stop $ 1 $ goes first on its way and stop $ n $ goes last). The stops are positioned on a straight line and their coordinates are $ 0=x_{1}<x_{2}<...<x_{n} $ .
Each day exactly $ m $ people use bus $ 62 $ . For each person we know the number of the stop where he gets on the bus and the number of the stop where he gets off the bus. A ticket from stop $ a $ to stop $ b $ ( $ a<b $ ) costs $ x_{b}-x_{a} $ rubles. However, the conductor can choose no more than one segment NOT TO SELL a ticket for. We mean that conductor should choose C and D (С
Input Format
The first line contains three integers $ n $ , $ m $ and $ c $ ( $ 2
Output Format
Print the single real number — the maximum expectation of the conductor's profit. Your answer will be considered correct if its absolute or relative error does not exceed $ 10^{-6} $ .
Namely: let's assume that your answer is $ a $ , and the answer of the jury is $ b $ . The checker program will consider your answer correct, if 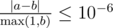.
Explanation/Hint
A comment to the first sample:
The first and third passengers get tickets from stop $ 1 $ to stop $ 2 $ . The second passenger doesn't get a ticket. There always is inspection on the segment $ 1 $ - $ 2 $ but both passengers have the ticket for it. There never is an inspection on the segment $ 2 $ - $ 3 $ , that's why the second passenger gets away with the cheating. Our total profit is $ (0+90/2+90/2)=90 $ .