CF1510F Fiber Shape

Imagine a board with $ n $ pins put into it, the $ i $ -th pin is located at $ (x_i, y_i) $ . For simplicity, we will restrict the problem to the case where the pins are placed in vertices of a convex polygon. Then, take a non-stretchable string of length $ l $ , and put it around all the pins. Place a pencil inside the string and draw a curve around the pins, trying to pull the string in every possible direction. The picture below shows an example of a string tied around the pins and pulled by a pencil (a point $ P $ ). 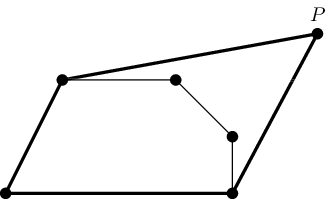Your task is to find an area inside this curve. Formally, for a given convex polygon $ S $ and a length $ l $ let's define a fiber shape $ F(S, l) $ as a set of points $ t $ such that the perimeter of the convex hull of $ S \cup \{t\} $ does not exceed $ l $ . Find an area of $ F(S, l) $ .

The first line contains two integers $ n $ and $ l $ ( $ 3 \le n \le 10^4 $ ; $ 1 \le l \le 8 \cdot 10^5 $ ) — the number of vertices of the polygon $ S $ and the length of the string. Next $ n $ lines contain integers $ x_i $ and $ y_i $ ( $ -10^5 \le x_i, y_i \le 10^5 $ ) — coordinates of polygon's vertices in counterclockwise order. All internal angles of the polygon are strictly less than $ \pi $ . The length $ l $ exceeds the perimeter of the polygon by at least $ 10^{-3} $ .

Output a single floating-point number — the area of the fiber shape $ F(S, l) $ . Your answer will be considered correct if its absolute or relative error doesn't exceed $ 10^{-6} $ .

The following pictures illustrate the example tests.