CF1510H Hard Optimization
题目描述
给定 $n$ 个线段 $[L_i, R_i]$,所有 $2n$ 个线段端点均为两两不同的整数。
这些线段构成“层状集”——任意两条线段要么互不相交,要么一条完全包含另一条。
你需要在每条线段 $[L_i, R_i]$ 内选择一个非空子线段 $[l_i, r_i]$,其中 $L_i \le l_i < r_i \le R_i$,使得所有选出的子线段两两不相交(但允许端点重合),并且使得它们长度之和 $\sum_{i=1}^n (r_i - l_i)$ 最大。
输入格式
第一行包含一个整数 $n$($1 \le n \le 2 \cdot 10^3$),表示线段的数量。
接下来的 $n$ 行,每行包含两个整数 $L_i$ 和 $R_i$($0 \le L_i < R_i \le 10^9$),表示第 $i$ 条线段的两个端点。
所有 $2n$ 个端点均为不同的整数。给定的线段集合是层状集。
输出格式
第一行输出最大可能的子线段长度和。
接下来的 $n$ 行,每行输出两个整数 $l_i$ 和 $r_i$($L_i \le l_i < r_i \le R_i$),表示第 $i$ 条线段中选出的子线段。
说明/提示
下方的示例输入输出配有示意图。
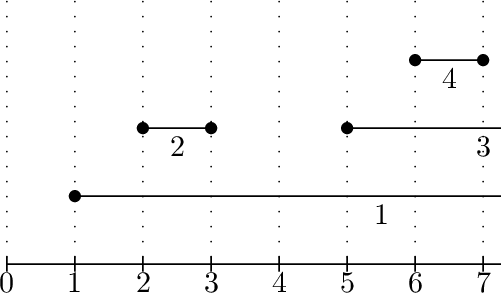
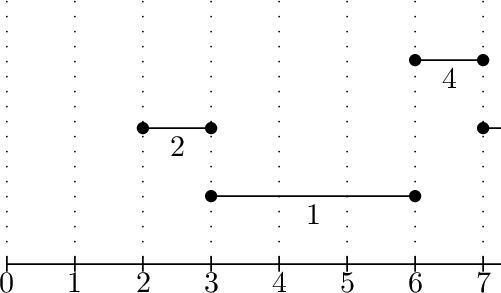
由 ChatGPT 4.1 翻译