CF1513D GCD and MST

You are given an array $ a $ of $ n $ ( $ n \geq 2 $ ) positive integers and an integer $ p $ . Consider an undirected weighted graph of $ n $ vertices numbered from $ 1 $ to $ n $ for which the edges between the vertices $ i $ and $ j $ ( $ i

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The first line of each test case contains two integers $ n $ ( $ 2 \leq n \leq 2 \cdot 10^5 $ ) and $ p $ ( $ 1 \leq p \leq 10^9 $ ) — the number of nodes and the parameter $ p $ . The second line contains $ n $ integers $ a_1, a_2, a_3, \dots, a_n $ ( $ 1 \leq a_i \leq 10^9 $ ). It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

Output $ t $ lines. For each test case print the weight of the corresponding graph.

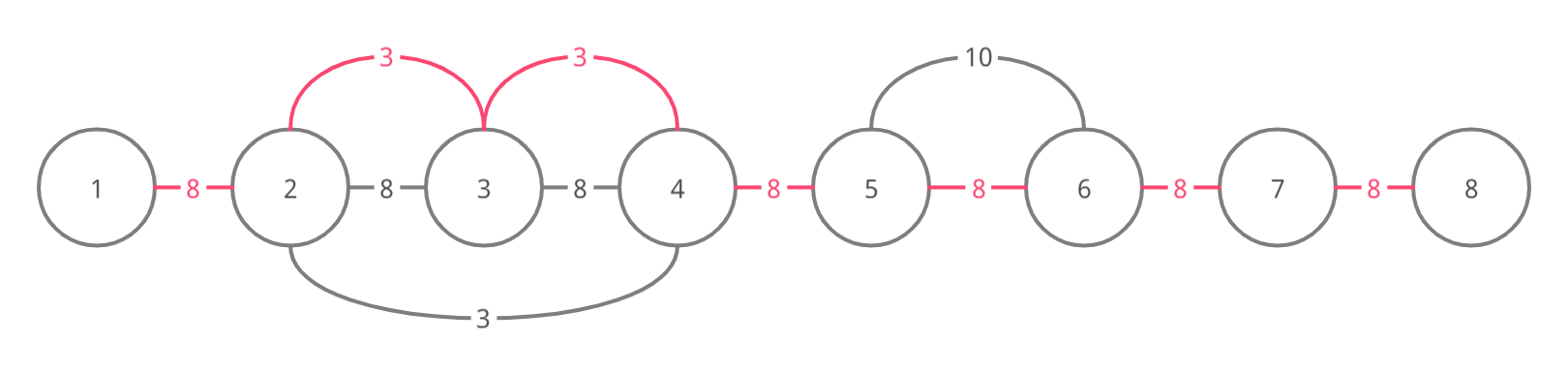
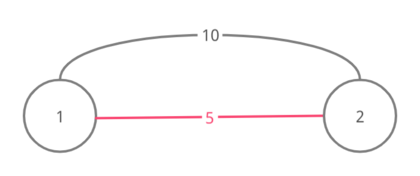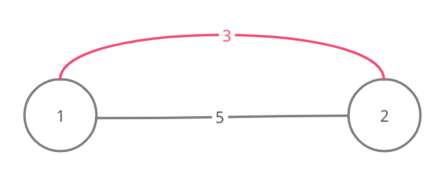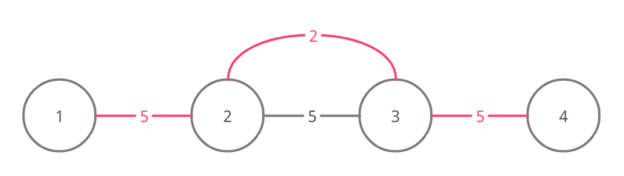Here are the graphs for the four test cases of the example (the edges of a possible MST of the graphs are marked pink): For test case 1 For test case 2 For test case 3 For test case 4