CF1517B Morning Jogging

2050 志愿者正在组织“奔跑吧！追逐朝阳”活动。活动将于 4 月 25 日上午 7:30 开始，参赛者需要完成云栖小镇周边的 6 公里跑道。 跑道上共有 $n+1$ 个检查点，编号为 $0, 1, \ldots, n$。每位参赛者必须从检查点 $0$ 出发，到达检查点 $n$ 结束。所有检查点都必须经过，不能跳过——也就是说，必须依次从检查点 $0$ 跑到 $1$，再从 $1$ 跑到 $2$，以此类推。具体可参考备注部分的图片。 在任意两个相邻检查点之间，有 $m$ 条不同的路径可供选择。对于任意 $1 \leq i \leq n$，从检查点 $i-1$ 到检查点 $i$，参赛者可以从 $m$ 条路径中选择一条。第 $i-1$ 到第 $i$ 个检查点之间第 $j$ 条路径的长度为 $b_{i,j}$，其中 $1 \leq j \leq m$，$1 \leq i \leq n$。 为了测试赛道，我们有 $m$ 位参赛者。每位参赛者都必须从检查点 $0$ 跑到检查点 $n$ 一次，且必须经过所有检查点。每一对相邻检查点之间的每一条路径都必须被恰好一位参赛者跑过。如果某位参赛者在第 $i-1$ 到第 $i$ 个检查点之间选择了长度为 $l_i$ 的路径（$1 \leq i \leq n$），那么他的疲劳度为 $\min_{i=1}^n l_i$，即他所选择的所有路径中最短的那一条的长度。 请为 $m$ 位参赛者合理分配路径，使得所有人的疲劳度之和最小。

每个测试点包含多组测试用例。第一行包含测试用例个数 $t$（$1 \leq t \leq 10\,000$）。接下来是每组测试用例的描述。 每组测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \leq n, m \leq 100$）。 接下来的 $n$ 行，每行包含 $m$ 个整数 $b_{i,1}, b_{i,2}, \ldots, b_{i,m}$（$1 \leq b_{i,j} \leq 10^9$）。 保证所有测试用例中 $n \cdot m$ 的总和不超过 $10^4$。

对于每组测试用例，输出 $n$ 行。第 $i$ 行的第 $j$ 个数表示第 $j$ 位参赛者从检查点 $i-1$ 跑到检查点 $i$ 时选择的路径长度。每行应恰好包含 $m$ 个整数，并且这 $m$ 个数应为 $b_{i,1}, \ldots, b_{i,m}$ 的一个排列（即每条路径只能被一位参赛者选择）。 如果有多种方案，输出任意一种均可。

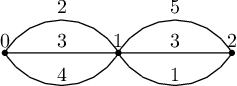
在第一个样例中，疲劳度之和为 $\min(2,5) + \min(3,3) + \min(4,1) = 6$。  在第二个样例中，疲劳度之和为 $\min(2,4,3) + \min(3,1,5) = 3$。 由 ChatGPT 4.1 翻译