CF1517C Fillomino 2
题目描述
Fillomino 是一道经典的逻辑谜题。(你不需要了解 Fillomino 也能解决本题。)在云栖镇的一间教室里,一些志愿者正在玩它的一个棋盘游戏变体:
给定一个 $n \times n$ 的棋盘。棋盘的行从上到下编号为 $1$ 到 $n$,列从左到右编号为 $1$ 到 $n$。位于第 $x$ 行第 $y$ 列的格子记作 $(x, y)$。棋盘的主对角线是所有 $(x, x)$($1 \le x \le n$)的格子。
在主对角线上写有 $\{1, 2, 3, \dots, n\}$ 的一个排列。每个格子上恰好写有一个数字。现在需要将主对角线及其下方的所有格子(共 $1+2+\ldots+n$ 个格子)划分为 $n$ 个连通区域,满足以下条件:
1. 每个区域必须是连通的。也就是说,从区域内任意一个格子出发,只经过该区域内的格子并每次移动到相邻格子,可以到达该区域内的任意其他格子。
2. 第 $x$ 个区域必须包含主对角线上数字为 $x$ 的格子($1 \le x \le n$)。
3. 第 $x$ 个区域包含的格子数必须恰好为 $x$($1 \le x \le n$)。
4. 主对角线及其下方的每个格子必须且仅属于一个区域。
输入格式
第一行包含一个整数 $n$($1 \le n \le 500$),表示棋盘的大小。
第二行包含 $n$ 个整数 $p_1, p_2, \ldots, p_n$,$p_i$ 表示在格子 $(i, i)$ 上写的数字。保证 $p_1, \ldots, p_n$ 是 $1$ 到 $n$ 的一个排列。
输出格式
如果不存在满足条件的划分,输出 $-1$。
否则,输出 $n$ 行。第 $i$ 行包含 $i$ 个数字。第 $j$ 个数字为 $x$,表示格子 $(i, j)$ 属于包含 $x$ 个格子的区域。
说明/提示
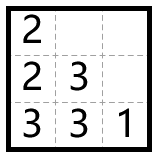
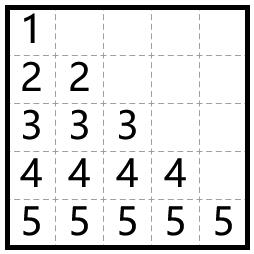
样例的解如下图所示:
由 ChatGPT 4.1 翻译