CF1519E Off by One

在一张无限大的平面上有 $n$ 个点。第 $i$ 个点的坐标为 $(x_i, y_i)$，其中 $x_i > 0$ 且 $y_i > 0$。这些坐标不一定是整数。 每次操作你可以进行如下步骤： - 选择两个不同的点 $a$ 和 $b$（$a \neq b$）； - 将点 $a$ 从 $(x_a, y_a)$ 移动到 $(x_a + 1, y_a)$ 或 $(x_a, y_a + 1)$； - 将点 $b$ 从 $(x_b, y_b)$ 移动到 $(x_b + 1, y_b)$ 或 $(x_b, y_b + 1)$； - 移除点 $a$ 和 $b$。 但是，只有当存在一条直线经过点 $a$ 的新坐标、点 $b$ 的新坐标以及 $(0, 0)$ 时，才能进行上述操作。 否则，操作无法进行，点 $a$ 和 $b$ 保持原坐标不变。 点的编号在移除后不会改变。被移除的点不能再被选中。注意，每次操作必须移动两个点，不能让它们保持原地不动。 你能进行的最多操作次数是多少？这些操作分别是哪些？ 如果有多种方案，输出任意一种均可。

第一行包含一个整数 $n$（$1 \le n \le 2 \cdot 10^5$），表示点的数量。 接下来的 $n$ 行，每行包含四个整数 $a_i, b_i, c_i, d_i$（$1 \le a_i, b_i, c_i, d_i \le 10^9$）。第 $i$ 个点的坐标为 $x_i = \frac{a_i}{b_i}$，$y_i = \frac{c_i}{d_i}$。

第一行输出一个整数 $c$，表示你能进行的最多操作次数。 接下来的 $c$ 行，每行输出两个整数 $a$ 和 $b$（$1 \le a, b \le n$，$a \neq b$），表示本次操作中被移除的两个点。对于每一对 $(a, b)$，应当存在一种移动方式，使得点 $a$ 和 $b$ 的新坐标与 $(0, 0)$ 共线。每个被移除的点不能再被选中。 如果有多种方案，输出任意一种均可。操作顺序和每次操作中点的顺序均可任意。

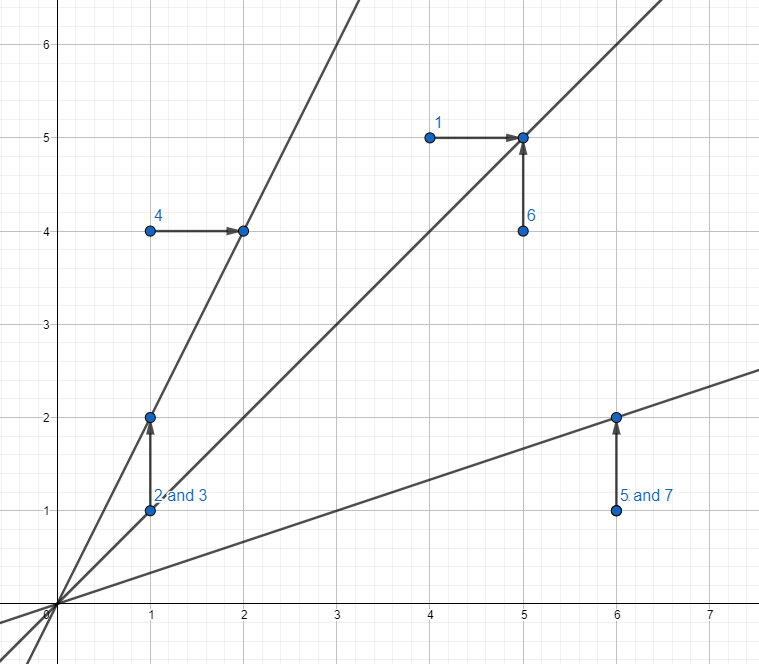
以下是第一个样例中被选中进行操作的点及其移动示意图：  由 ChatGPT 4.1 翻译