CF1520G To Go Or Not To Go?
题目描述
给定一个 $n\times{m}$ 的网格,每个格子 $(i,j)$ 都有一个整数参数 $a_{ij}(-1\leq a_{ij}\leq10^9)$ ,
$a_{ij}=-1$ 表示这个格子不能通过;否则,这个格子可以通过,若 $a_{ij}>0$ 则表示这个格子内有一个传送门。
现在小D想要从 $(1,1)$ 移动到到 $(n,m)$ ,它可以以如下两种方式移动:
- 在任意两个相邻且参数均不为$-1$的格子间移动,花费为 $w$ ;
- 在有传送门的两个格子 $(i,j)$ 和 $(x,y)$ 间移动,花费为 $a_{ij}+a_{xy}$ 。
求小D所需的最小花费。
输入格式
第一行输入三个整数 $n,m,w$ $(1\leq n,m\leq2\times{10^3}$ ,$1\leq w\leq10^9)$ 。
接下来 $n$ 行,每行 $m$ 个数,第 $i$ 行的第 $j$ 个数表示 $a_{ij}$ 。
输出格式
输出小D的最小花费。若她无法由 $(1,1)$ 行到 $(n,m)$ ,输出 $-1$ 。
说明/提示
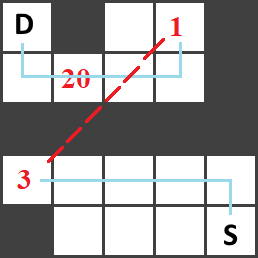
Explanation for the first sample: