CF1525C Robot Collisions

有 $n$ 个机器人沿着 OX 轴行驶。轴上有两堵墙：一堵在坐标 $0$，另一堵在坐标 $m$。 第 $i$ 个机器人起始于整数坐标 $x_i$（$0 < x_i < m$），并以每秒 $1$ 单位的速度向左（朝 $0$ 方向）或向右行驶。没有两个机器人起始于同一坐标。 每当机器人到达一堵墙时，它会立刻掉头，以相同的速度向相反方向继续行驶。 每当若干机器人在同一个整数坐标相遇时，它们会发生碰撞并化为尘埃。一旦机器人爆炸，它就不会再与其他机器人发生碰撞。注意，如果若干机器人在非整数坐标相遇，则什么也不会发生。 对于每个机器人，判断它是否会爆炸，如果会，请输出其爆炸的时间，否则输出 $-1$。

第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。 接下来是 $t$ 组测试用例。 每组测试用例的第一行包含两个整数 $n$ 和 $m$（$1 \le n \le 3 \cdot 10^5$，$2 \le m \le 10^8$），分别表示机器人的数量和右侧墙的坐标。 第二行包含 $n$ 个整数 $x_1, x_2, \dots, x_n$（$0 < x_i < m$），表示每个机器人的起始坐标。 第三行包含 $n$ 个用空格分隔的字符 'L' 或 'R'，表示每个机器人的初始行驶方向（'L' 表示向左，'R' 表示向右）。 同一测试用例中所有 $x_i$ 均不相同。 所有测试用例中 $n$ 的总和不超过 $3 \cdot 10^5$。

对于每组测试用例，输出 $n$ 个整数，第 $i$ 个整数表示第 $i$ 个机器人爆炸的时间，如果不会爆炸则输出 $-1$。

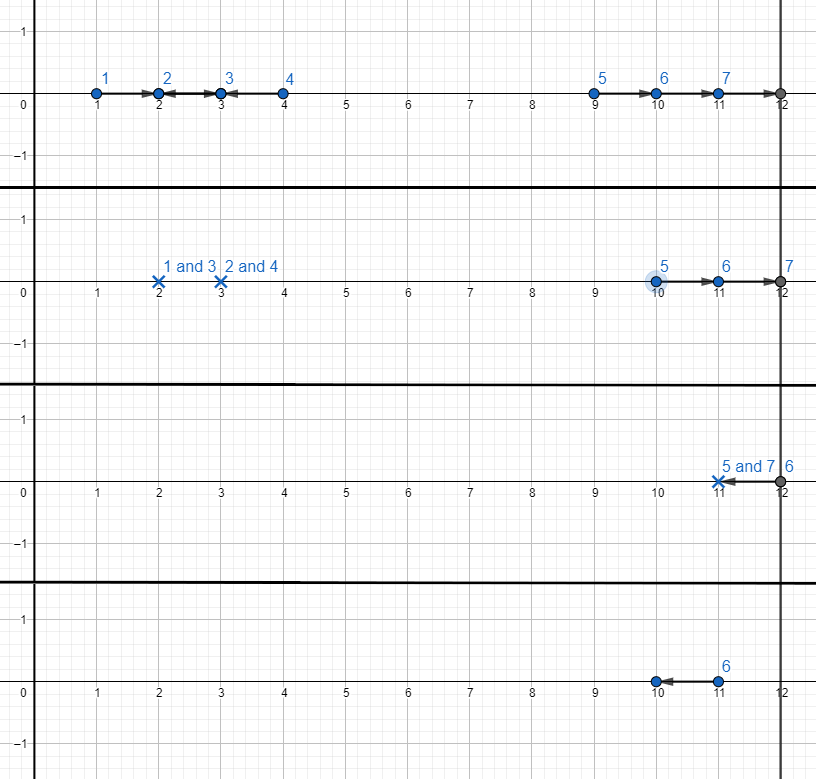
以下是第一个测试用例在第 $0, 1, 2, 3$ 秒的示意图：  注意，机器人 $2$ 和 $3$ 不会发生碰撞，因为它们在 $2.5$ 这个非整数点相遇。 第 $3$ 秒后，机器人 $6$ 会一直行驶下去，因为没有其他机器人与其碰撞。 由 ChatGPT 4.1 翻译