CF1527D MEX Tree

给定一棵有 $n$ 个节点的树，节点编号从 $0$ 到 $n-1$。对于每个 $k$，$0 \leq k \leq n$，你需要统计有多少无序点对 $(u, v)$，$u \neq v$，使得从 $u$ 到 $v$ 的最短路径（包括端点）上所有节点编号的 MEX 等于 $k$。 一个整数序列的 MEX 是不属于该序列的最小非负整数。

第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 2 \cdot 10^{5}$）。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$0 \leq u,v \leq n-1$），表示树中的一条边（$u \neq v$）。 保证给出的边构成一棵树。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^{5}$。

对于每个测试用例，输出 $n+1$ 个整数，第 $k$ 个整数表示树中所有路径的数量，使得该路径上所有节点编号的 MEX 等于 $k$，$k$ 从 $0$ 到 $n$。

1. 对于样例 $1$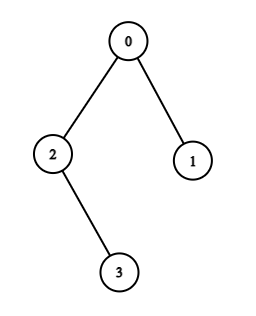， - 当 $k=0$ 时，有 $1$ 条路径，即从 $2$ 到 $3$，因为 $MEX([2, 3]) = 0$。 - 当 $k=1$ 时，有 $2$ 条路径，分别是 $0$ 到 $2$（$MEX([0, 2]) = 1$）和 $0$ 到 $3$（$MEX([0, 2, 3]) = 1$）。 - 当 $k=2$ 时，有 $1$ 条路径，即 $0$ 到 $1$，因为 $MEX([0, 1]) = 2$。 - 当 $k=3$ 时，有 $1$ 条路径，即 $1$ 到 $2$，因为 $MEX([1, 0, 2]) = 3$。 - 当 $k=4$ 时，有 $1$ 条路径，即 $1$ 到 $3$，因为 $MEX([1, 0, 2, 3]) = 4$。 2. 对于样例 $2$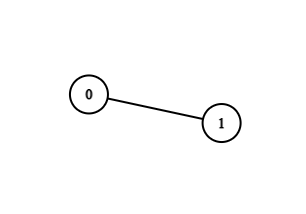， - 当 $k=0$ 时，没有这样的路径。 - 当 $k=1$ 时，没有这样的路径。 - 当 $k=2$ 时，有 $1$ 条路径，即 $0$ 到 $1$，因为 $MEX([0, 1]) = 2$。 由 ChatGPT 4.1 翻译