CF1527D MEX Tree

You are given a tree with $ n $ nodes, numerated from $ 0 $ to $ n-1 $ . For each $ k $ between $ 0 $ and $ n $ , inclusive, you have to count the number of unordered pairs $ (u,v) $ , $ u \neq v $ , such that the MEX of all the node labels in the shortest path from $ u $ to $ v $ (including end points) is $ k $ . The MEX of a sequence of integers is the smallest non-negative integer that does not belong to the sequence.

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 2 \cdot 10^{5} $ ). The next $ n-1 $ lines of each test case describe the tree that has to be constructed. These lines contain two integers $ u $ and $ v $ ( $ 0 \le u,v \le n-1 $ ) denoting an edge between $ u $ and $ v $ ( $ u \neq v $ ). It is guaranteed that the given edges form a tree. It is also guaranteed that the sum of $ n $ for all test cases does not exceed $ 2 \cdot 10^{5} $ .

For each test case, print $ n+1 $ integers: the number of paths in the tree, such that the MEX of all the node labels in that path is $ k $ for each $ k $ from $ 0 $ to $ n $ .

1. In example case $ 1 $ , 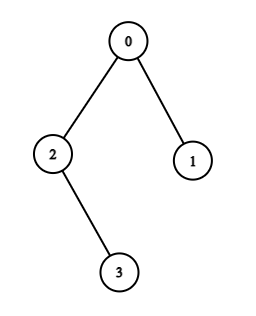 - For $ k = 0 $ , there is $ 1 $ path that is from $ 2 $ to $ 3 $ as $ MEX([2, 3]) = 0 $ . - For $ k = 1 $ , there are $ 2 $ paths that is from $ 0 $ to $ 2 $ as $ MEX([0, 2]) = 1 $ and $ 0 $ to $ 3 $ as $ MEX([0, 2, 3]) = 1 $ . - For $ k = 2 $ , there is $ 1 $ path that is from $ 0 $ to $ 1 $ as $ MEX([0, 1]) = 2 $ . - For $ k = 3 $ , there is $ 1 $ path that is from $ 1 $ to $ 2 $ as $ MEX([1, 0, 2]) = 3 $ - For $ k = 4 $ , there is $ 1 $ path that is from $ 1 $ to $ 3 $ as $ MEX([1, 0, 2, 3]) = 4 $ . 2. In example case $ 2 $ , 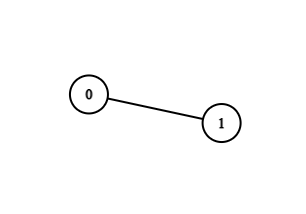 - For $ k = 0 $ , there are no such paths. - For $ k = 1 $ , there are no such paths. - For $ k = 2 $ , there is $ 1 $ path that is from $ 0 $ to $ 1 $ as $ MEX([0, 1]) = 2 $ .