CF1531C Симметричный амфитеатр

Все готовятся к VK Fest 2021! Для того, чтобы зрителям была лучше видна главная сцена, планируется построить амфитеатр. В этой задаче мы будем рассматривать его сбоку — схематично он будет иметь форму лестницы из $ n $ одинаковых квадратов. Лестница — это одна или более башен квадратов, выстроенных в ряд, где высоты башен невозрастают слева направо. На следующем рисунке можно видеть три разные фигуры из $ 12 $ квадратов. Первые две фигуры — лестницы, а третья — нет. 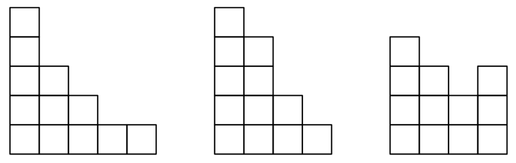Из эстетических соображений было решено, что амфитеатр должен быть симметричным. Формально, амфитеатр называется симметричным, если при отражении его схемы относительно прямой $ x = y $ получается тот же самый рисунок (где ось $ x $ направлена слева направо, а ось $ y $ — снизу вверх). Например, первая лестница на рисунке выше — симметричная, а вторая — нет. 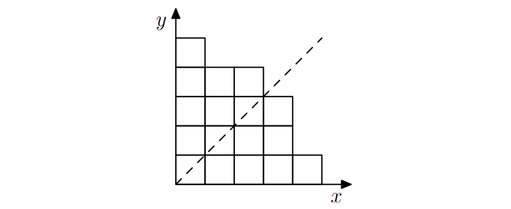Кроме того, амфитеатр должен быть максимально компактным — а именно, сторона минимального квадрата, внутрь которого можно его поместить, должна быть как можно меньше. По заданному числу $ n $ нарисуйте схему амфитеатра из ровно $ n $ квадратов, удовлетворяющую всем условиям.

В единственной строке задано одно целое число $ n $ ( $ 1 \le n \le 100 $ ) — число квадратов, из которых нужно составить схему амфитеатра.

Если не существует схемы амфитеатра из $ n $ квадратов, выведите единственное число $ -1 $ . Иначе в первой строке выведите целое число $ m $ — минимальное возможное число строк и столбцов в схеме амфитеатра. Далее выведите $ m $ строк, описывающих схему. Каждая строка должна содержать ровно $ m $ символов 'o' (строчная латинская буква) или '.', где 'o' описывает построенный квадрат, а '.' — пустое место. Схема амфитеатра должна состоять ровно из $ n $ символов 'o'. Ячейка в левом нижнем углу должна содержать квадрат. Если возможных ответов с минимальным $ m $ несколько, выведите любой из них.