CF1534B Histogram Ugliness
题目描述
小 Dormi 收到了一个有 $n$ 根柱子的直方图作为圣诞礼物,每根柱子的高度分别为 $a_1, a_2, \ldots, a_n$。然而,他越玩越觉得这个直方图不够完美,于是今天他想按照自己的喜好对其进行修改。
小 Dormi 可以对直方图进行如下操作任意多次:
- 选择一个下标 $i$($1 \le i \le n$),且 $a_i > 0$,然后令 $a_i := a_i - 1$。
小 Dormi 定义直方图的“丑陋度”为:对直方图进行若干次操作后,其轮廓的竖直长度之和与他所做操作次数之和的总和。为了让直方图尽可能完美,他希望在经过若干次操作后,使丑陋度最小。
然而,由于直方图很大,小 Dormi 难以最小化丑陋度。作为他的哥哥,请你帮他求出每个直方图能达到的最小丑陋度。
例如,考虑一个有 $4$ 根柱子的直方图,高度分别为 $4,8,9,6$:
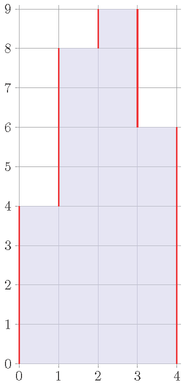
蓝色区域表示直方图,红色线段表示轮廓的竖直部分。当前轮廓的竖直长度为 $4+4+1+3+6=18$,如果不进行任何操作,丑陋度就是 $18$。
但小 Dormi 可以对第 $2$ 根柱子操作一次,对第 $3$ 根柱子操作两次,得到高度为 $4,7,7,6$ 的直方图:

此时轮廓的竖直长度为 $4+3+1+6=14$,操作次数为 $3$,丑陋度为 $14+3=17$。可以证明这是最优解。
输入格式
每组测试数据包含多个测试用例。第一行包含一个整数 $t$($1 \le t \le 10^4$),表示测试用例的数量。接下来是每个测试用例的描述。
每个测试用例的第一行包含一个整数 $n$($1 \le n \le 4 \times 10^5$)。
第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$($0 \le a_i \le 10^9$)。
保证所有测试用例中 $n$ 的总和不超过 $4 \times 10^5$。
输出格式
对于每个测试用例,输出一个整数,表示小 Dormi 能够达到的最小丑陋度。
说明/提示
样例 $1$ 即为题目描述中的例子。
样例 $2$ 的初始直方图如下:
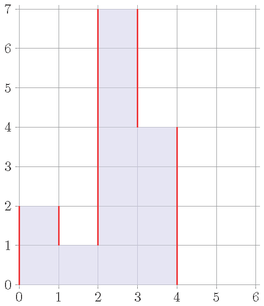
当前丑陋度为 $2+1+6+3+4=16$。
对第 $1$ 根柱子操作一次,第 $3$ 根柱子操作六次,第 $4$ 根柱子操作三次,可以得到高度为 $1,1,1,1,0,0$ 的直方图:
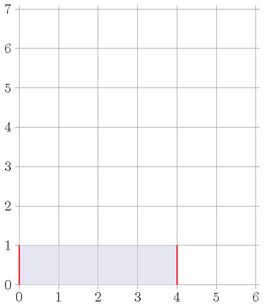
此时轮廓的竖直长度为 $1+1=2$,操作次数为 $1+6+3=10$,最终丑陋度为 $2+10=12$。可以证明这是最优解。
由 ChatGPT 4.1 翻译