CF1534F2 Falling Sand (Hard Version)

这是该问题的困难版本。不同版本的区别在于 $a_i$ 的约束条件。只有当所有版本的问题都被解决时，你才能进行 hack。 Little Dormi 最近从朋友那里收到了一道谜题，需要你的帮助来解决它。 这个谜题由一个竖直的棋盘组成，棋盘有 $n$ 行 $m$ 列，每个格子要么是空的，要么填有一块沙子，并且给定 $m$ 个非负整数 $a_1,a_2,\ldots,a_m$（$0 \leq a_i \leq n$）。在本题版本中，$a_i$ 总是不大于第 $i$ 列中沙子的数量。 当某个格子中的沙块被扰动时，这块沙子会从它所在的格子落到该列底部的沙子计数器中（每列都有一个沙子计数器）。在沙块下落的过程中，所有与下落沙块相邻的其他沙块也会被扰动并开始下落。具体来说，在格子 $(i,j)$ 被扰动的沙块会穿过该列中从 $(i,j)$ 到底部的所有格子，并在途中扰动所有相邻的格子。这里，相邻格子指的是 $(i-1,j)$、$(i,j-1)$、$(i+1,j)$ 和 $(i,j+1)$（如果它们在棋盘内）。注意，新下落的沙块也会继续扰动其它沙块。 每次操作你可以扰动任意一块沙子。当每一列的沙子计数器中至少有 $a_i$ 块沙子时，谜题就被解决了。 你的任务是求出解决这个谜题所需的最少操作次数。注意，Little Dormi 保证给你的谜题一定有解。

第一行包含两个用空格分隔的正整数 $n$ 和 $m$（$1 \leq n \cdot m \leq 400\,000$）。 接下来的 $n$ 行，每行包含 $m$ 个字符，描述棋盘的每一行。如果某个字符为 '.'，则对应格子为空；如果为 '\#'，则该格子中有一块沙子。 最后一行包含 $m$ 个非负整数 $a_1,a_2,\ldots,a_m$（$0 \leq a_i \leq n$），表示每一列底部计数器中至少需要落下的沙子数。在本题版本中，$a_i$ 总是不大于第 $i$ 列中沙子的数量。

输出一个非负整数，表示解决谜题所需的最少操作次数。

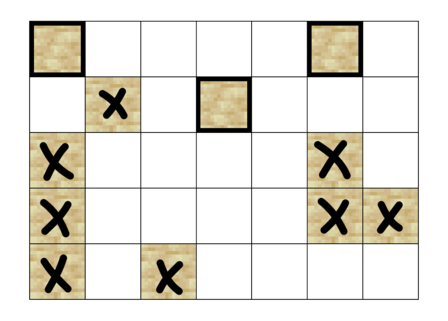
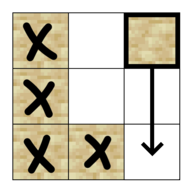
例如，第 $1$ 个样例中，通过扰动第一行最左边第一列和第六列的两块沙子，以及第二行第四列的那块沙子，可以使每一列都达到所需的沙子数量。可以证明，少于 $3$ 次操作无法完成，因此答案为 $3$。下图为第一个样例的谜题。  例如，第 $2$ 个样例中，通过扰动第一行最右边一列的格子，可以使棋盘上所有沙子都落入底部计数器。因此答案为 $1$。下图为第二个样例的谜题。  例如，第 $3$ 个样例中，通过扰动第一行最右边一列的格子，可以使每一列都达到所需的沙子数量。可以证明，少于 $1$ 次操作无法完成，因此答案为 $1$。下图为第三个样例的谜题。  由 ChatGPT 4.1 翻译