CF1534H Lost Nodes

**这是一道交互题。** 小 Ericyi 因为晋级了 IOI，所以收到了朋友们送的一份礼物 —— 一棵有 $n$ 个节点的树！ 在飞往 IOI 的途中，百无聊赖的 Ericyi 和小 Yvonne 玩起了一个与这棵树有关的游戏。Yvonne 首先在树上选定两个节点 $a$ 和 $b$（可以相同），然后挑出一条从 $a$ 到 $b$ 的路径上的某个节点 $f$（包含 $a,b$ 本身）作为提示，告诉给 Ericyi。 接着，Ericyi 可以反复进行如下的询问操作： - 如果我将整棵树以节点 $r$ 为根（$r$ 由 Ericyi 选择），那么 $a$ 和 $b$ 的 最近公共祖先（LCA） 是哪个节点？ Ericyi 的目标是找出这两个被隐藏的节点 $a$ 和 $b$。 但 Yvonne 觉得游戏太简单了，于是在游戏开始前，要求 Ericyi 先回答这样一个问题： “若你采取最优策略，在所有可能的 $a, b, f$ 情况下，你最多需要多少次询问才能确定 $a$ 和 $b$？” Ericyi 所回答的最大查询次数 $k$，将会是他在之后的游戏中能使用的最多查询次数。一旦他作答，$a,b,f$ 就会固定，不能更改。 **注意：** 在整个交互过程中，树的结构、$a$、$b$ 和 $f$ 都在最开始就固定，且**不会因为查询改变。**

无。

首先，读入一个整数 $n$（$1 \le n \le 10^5$），表示树的节点数。 接下来 $n-1$ 行，每行两个整数 $u,v$（$1 \le u,v \le n, u \ne v$），表示一条树边，保证这些边构成一棵树。 然后你需要输出一个整数 $k$（$0 \le k \le n$），表示你估算出的在最坏情况下所需的最小查询次数上界。请输出换行并刷新输出缓冲区。 之后你会读入一个整数 $f$（$1 \le f \le n$），表示提示节点，是从 $a$ 到 $b$ 的路径上的某个节点。 接下来你可以进行至多 $k$ 次交互式询问，每次格式如下： ``` ? r ``` 表示将树以节点 $r$ 为根，并请求此时 $a$ 与 $b$ 的最近公共祖先节点编号。你将收到一个整数 $x$（$1 \le x \le n$），表示 LCA($a,b$) 在以 $r$ 为根时的结果。 当你确定 $a$ 和 $b$ 后，请按如下格式输出答案： ``` ! a b ``` $a,b$ 顺序可以颠倒。输出后请刷新并立即正常结束程序。 特别注意：每次输出后都必须换行并刷新输出缓冲区，否则将收到 Idleness limit exceeded 判定！ 常用语言刷新方式： - C++：`fflush(stdout);` 或 `cout.flush();` - Java：`System.out.flush();` - Python：`sys.stdout.flush()` - 其他语言请参考相关文档。 如果你输出非法格式、或超过了 $k$ 次查询，将被立即终止并判定为 Wrong Answer。

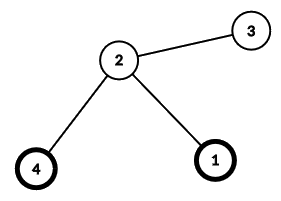
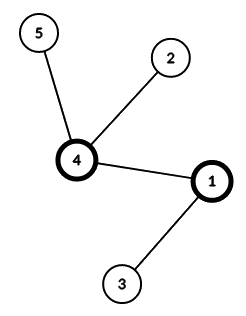
下面是样例 1 中的树结构，节点 $a$ 和 $b$ 已高亮标出：  注意：输出的 $a$ 和 $b$ 可以颠倒顺序，任意顺序均可。 为了方便理解，下面列出了以每个节点 $1,2,\ldots,n$ 作为根时的查询结果（即 $\text{LCA}(a,b)$）： * 以 1 为根：LCA = 1 * 以 2 为根：LCA = 2 * 以 3 为根：LCA = 2 * 以 4 为根：LCA = 4 --- 下面是样例 2 中的树结构，同样高亮了节点 $a$ 和 $b$：  以下是本样例中对每个节点 $1,2,\ldots,n$ 进行查询时的结果： * 以 1 为根：LCA = 1 * 以 2 为根：LCA = 4 * 以 3 为根：LCA = 1 * 以 4 为根：LCA = 4 * 以 5 为根：LCA = 4