CF1535D Playoff Tournament

$ 2^k $ teams participate in a playoff tournament. The tournament consists of $ 2^k - 1 $ games. They are held as follows: first of all, the teams are split into pairs: team $ 1 $ plays against team $ 2 $ , team $ 3 $ plays against team $ 4 $ (exactly in this order), and so on (so, $ 2^{k-1} $ games are played in that phase). When a team loses a game, it is eliminated, and each game results in elimination of one team (there are no ties). After that, only $ 2^{k-1} $ teams remain. If only one team remains, it is declared the champion; otherwise, $ 2^{k-2} $ games are played: in the first one of them, the winner of the game " $ 1 $ vs $ 2 $ " plays against the winner of the game " $ 3 $ vs $ 4 $ ", then the winner of the game " $ 5 $ vs $ 6 $ " plays against the winner of the game " $ 7 $ vs $ 8 $ ", and so on. This process repeats until only one team remains. 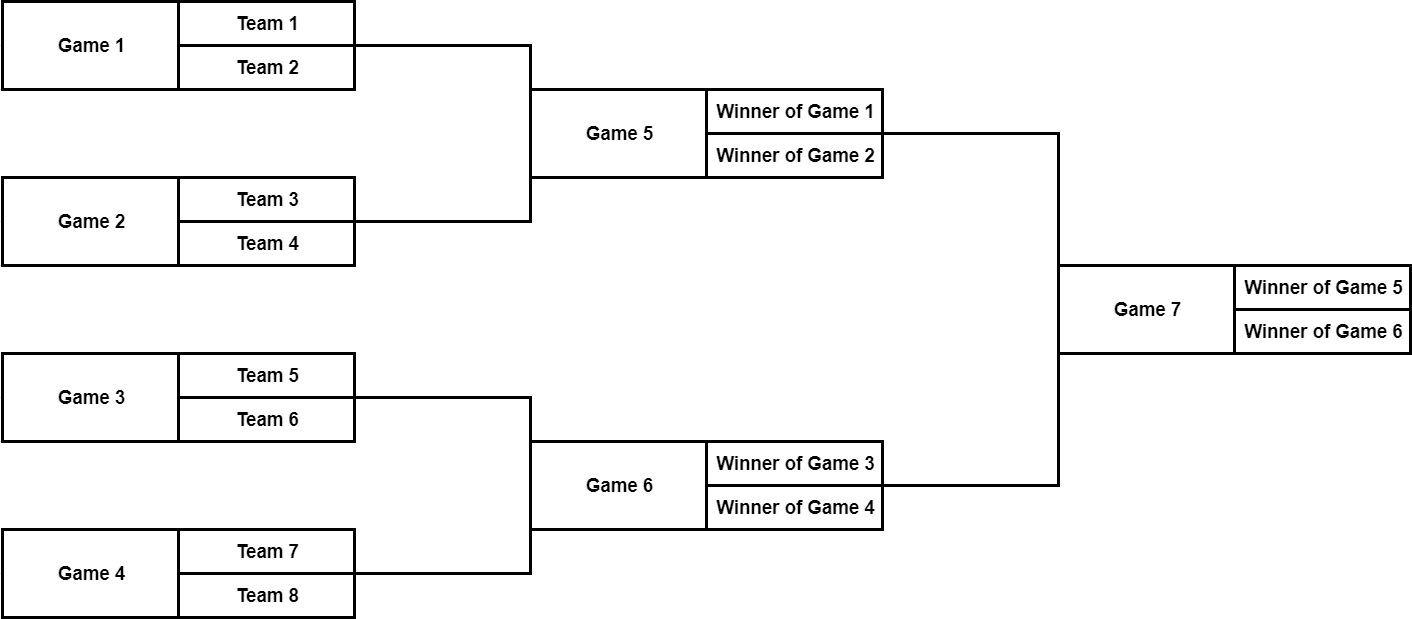For example, this picture describes the chronological order of games with $ k = 3 $ : Let the string $ s $ consisting of $ 2^k - 1 $ characters describe the results of the games in chronological order as follows: - if $ s_i $ is 0, then the team with lower index wins the $ i $ -th game; - if $ s_i $ is 1, then the team with greater index wins the $ i $ -th game; - if $ s_i $ is ?, then the result of the $ i $ -th game is unknown (any team could win this game). Let $ f(s) $ be the number of possible winners of the tournament described by the string $ s $ . A team $ i $ is a possible winner of the tournament if it is possible to replace every ? with either 1 or 0 in such a way that team $ i $ is the champion. You are given the initial state of the string $ s $ . You have to process $ q $ queries of the following form: - $ p $ $ c $ — replace $ s_p $ with character $ c $ , and print $ f(s) $ as the result of the query.

The first line contains one integer $ k $ ( $ 1 \le k \le 18 $ ). The second line contains a string consisting of $ 2^k - 1 $ characters — the initial state of the string $ s $ . Each character is either ?, 0, or 1. The third line contains one integer $ q $ ( $ 1 \le q \le 2 \cdot 10^5 $ ) — the number of queries. Then $ q $ lines follow, the $ i $ -th line contains an integer $ p $ and a character $ c $ ( $ 1 \le p \le 2^k - 1 $ ; $ c $ is either ?, 0, or 1), describing the $ i $ -th query.

For each query, print one integer — $ f(s) $ .