CF1537F Figure Fixing

你有一个由 $n$ 个节点和 $m$ 条边组成的连通无向图。第 $i$ 个节点有一个初始值 $v_i$ 和一个目标值 $t_i$。 每次操作，你可以选择一条边 $(i, j)$，并将某个整数 $k$ 加到 $v_i$ 和 $v_j$ 上，其中 $k$ 可以是任意整数，特别地，$k$ 可以为负数。 你的任务是判断，是否可以通过有限次（可以为零次）这样的操作，使得对于每个节点 $i$，都有 $v_i = t_i$。

第一行包含一个整数 $t$（$1 \leq t \leq 1000$），表示测试用例的数量。接下来是 $t$ 组测试用例。 每组测试用例的第一行包含两个整数 $n$ 和 $m$（$2 \leq n \leq 2 \cdot 10^5$，$n-1 \leq m \leq \min(2 \cdot 10^5, \frac{n(n-1)}{2})$），分别表示节点数和边数。 第二行包含 $n$ 个整数 $v_1, \ldots, v_n$（$-10^9 \leq v_i \leq 10^9$），表示每个节点的初始值。 第三行包含 $n$ 个整数 $t_1, \ldots, t_n$（$-10^9 \leq t_i \leq 10^9$），表示每个节点的目标值。 接下来的 $m$ 行，每行包含两个整数 $i$ 和 $j$，表示节点 $i$ 和节点 $j$ 之间有一条边（$1 \leq i, j \leq n$，$i \ne j$）。 保证图是连通的，且任意一对节点之间最多只有一条边。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$，$m$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，如果可以通过若干次操作使每个节点都达到目标值，输出 "YES"；否则输出 "NO"。

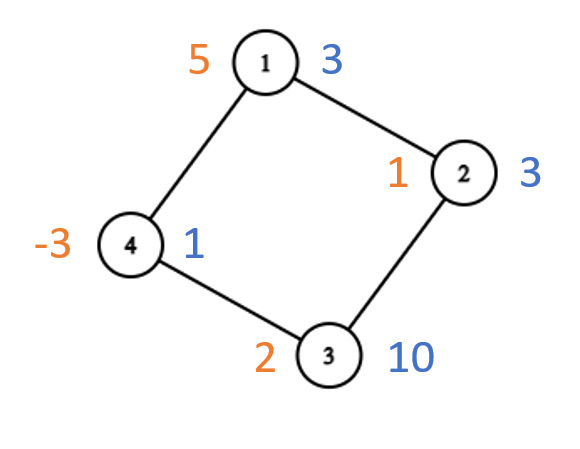
以下是第一个测试用例的可视化（橙色为初始值，蓝色为目标值）：  一种可能的操作顺序如下： - 操作 $1$：对节点 $2$ 和 $3$ 加 $2$。 - 操作 $2$：对节点 $1$ 和 $4$ 加 $-2$。 - 操作 $3$：对节点 $3$ 和 $4$ 加 $6$。 最终我们可以看到，总共对节点 $1$ 加了 $-2$，对节点 $2$ 加了 $2$，对节点 $3$ 加了 $8$，对节点 $4$ 加了 $4$，刚好使每个节点达到目标值。 对于第二个测试用例的图，不可能达到目标值。 由 ChatGPT 4.1 翻译