CF1543E The Final Pursuit
题目描述
你终于击败了 Razor,现在你成为了最受通缉的街头赛车手。警官 Cross 派出了全部警力对你展开致命追捕。幸运的是,你找到了一个藏身之处,但你担心 Cross 和他的部队最终会找到你。为了增加生存几率,你想对你的 BMW M3 GTR 进行调校和重新喷漆。
可以将这辆车想象成一个经过排列的 $n$ 维超立方体。一个简单的 $n$ 维超立方体是一个无向无权图,递归地构造如下:
- 取两个简单的 $(n-1)$ 维超立方体,一个顶点编号为 $0$ 到 $2^{n-1}-1$,另一个顶点编号为 $2^{n-1}$ 到 $2^n-1$。一个简单的 $0$ 维超立方体仅为一个顶点。
- 对于每个 $0\leq i < 2^{n-1}$,在顶点 $i$ 和 $i+2^{n-1}$ 之间添加一条边。
一个经过排列的 $n$ 维超立方体是通过对简单 $n$ 维超立方体的顶点编号进行任意排列得到的。
下图给出了一个简单和一个经过排列的 $3$ 维超立方体的例子:
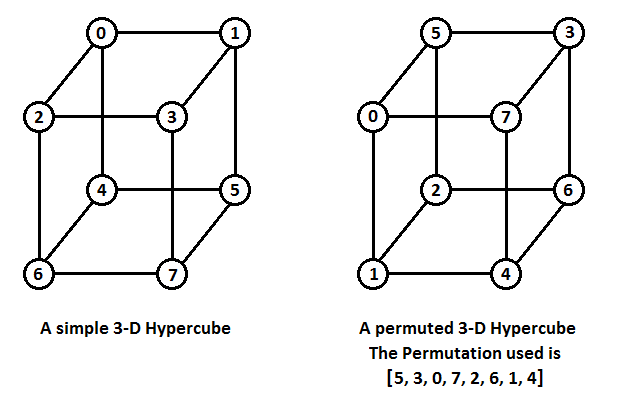
注意,一个经过排列的 $n$ 维超立方体具有如下性质:
- 恰好有 $2^n$ 个顶点。
- 恰好有 $n\cdot 2^{n-1}$ 条边。
- 每个顶点恰好与 $n$ 个其他顶点相连。
- 没有自环或重边。
设用于将简单 $n$ 维超立方体变换为输入中给定的经过排列的 $n$ 维超立方体的排列为 $P$。在对车辆进行改装前,你希望找出这个排列,以便在出现问题时可以恢复车辆。但这还不是全部。
你有 $n$ 种不同的颜色,编号为 $0$ 到 $n-1$。你希望对这个经过排列的 $n$ 维超立方体的顶点进行染色,使得对于每一个顶点 $u$($0\leq u < 2^n$)和每一种颜色 $c$($0\leq c < n$),都至少存在一个与 $u$ 相邻的顶点 $v$,其颜色为 $c$。换句话说,从每个顶点出发,只需移动到一个相邻顶点,就必须能到达任意一种颜色的顶点。
给定一个经过排列的 $n$ 维超立方体,请找出任意一个有效的排列 $P$ 以及一种满足条件的染色方案。
输入格式
输入的第一行包含一个整数 $t$($1\leq t\leq 4096$),表示测试用例的数量。
对于每个测试用例,第一行包含一个整数 $n$($1\leq n\leq 16$)。
接下来的 $n\cdot 2^{n-1}$ 行,每行包含两个整数 $u$ 和 $v$($0\leq u, v < 2^n$),表示在编号为 $u$ 和 $v$ 的顶点之间有一条边。
保证输入描述的图是一个经过排列的 $n$ 维超立方体。
另外,保证所有测试用例中 $2^n$ 的总和不超过 $2^{16}=65536$。
输出格式
对于每个测试用例,输出两行。
第一行输出一个长度为 $2^n$ 的排列 $P$,该排列可将简单 $n$ 维超立方体变换为输入中给定的经过排列的 $n$ 维超立方体。如果有多种答案,输出任意一种。
第二行输出染色方案。如果不存在满足条件的染色方案,输出 $-1$。否则,输出一行 $2^n$ 个用空格分隔的整数,第 $i$ 个整数表示输入中编号为 $i-1$ 的顶点的颜色。如果有多种答案,输出任意一种。
说明/提示
第一组测试数据的染色方案和排列超立方体如下图所示:
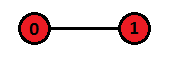
第二组测试数据的染色方案和排列超立方体如下图所示:
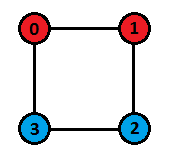
第三组测试数据的排列超立方体如题面所示,但可以证明不存在满足条件的染色方案。注意,其他一些排列如 $[0, 5, 7, 3, 1, 2, 4, 6]$ 和 $[0, 1, 5, 2, 7, 4, 3, 6]$ 也会得到相同的排列超立方体。
由 ChatGPT 4.1 翻译