CF1547A Shortest Path with Obstacle

There are three cells on an infinite 2-dimensional grid, labeled $ A $ , $ B $ , and $ F $ . Find the length of the shortest path from $ A $ to $ B $ if: - in one move you can go to any of the four adjacent cells sharing a side; - visiting the cell $ F $ is forbidden (it is an obstacle).

The first line contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the input. Then $ t $ test cases follow. Before each test case, there is an empty line. Each test case contains three lines. The first one contains two integers $ x_A, y_A $ ( $ 1 \le x_A, y_A \le 1000 $ ) — coordinates of the start cell $ A $ . The second one contains two integers $ x_B, y_B $ ( $ 1 \le x_B, y_B \le 1000 $ ) — coordinates of the finish cell $ B $ . The third one contains two integers $ x_F, y_F $ ( $ 1 \le x_F, y_F \le 1000 $ ) — coordinates of the forbidden cell $ F $ . All cells are distinct. Coordinate $ x $ corresponds to the column number and coordinate $ y $ corresponds to the row number (see the pictures below).

Output $ t $ lines. The $ i $ -th line should contain the answer for the $ i $ -th test case: the length of the shortest path from the cell $ A $ to the cell $ B $ if the cell $ F $ is not allowed to be visited.

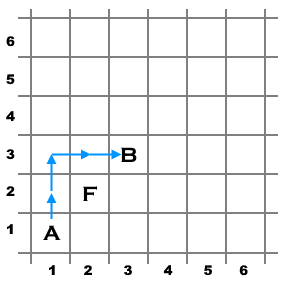An example of a possible shortest path for the first test case. 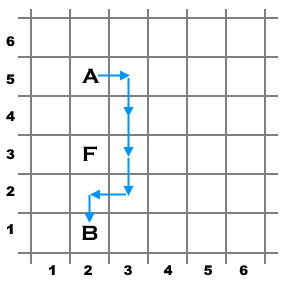An example of a possible shortest path for the second test case.