CF1547E Air Conditioners

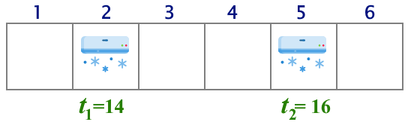
在一条长度为 $n$ 的狭长地带上，有 $k$ 台空调：第 $i$ 台空调放置在第 $a_i$ 个格子（$1 \le a_i \le n$）。同一个格子不能放置两台或以上的空调（即所有 $a_i$ 互不相同）。 每台空调有一个参数：温度。第 $i$ 台空调的温度为 $t_i$。 如下图所示，是长度为 $n=6$ 的狭长地带，其中 $k=2$，$a=[2,5]$，$t=[14,16]$。  对于每个格子 $i$（$1 \le i \le n$），请计算该格子的温度，其计算公式为 $$ \min_{1 \le j \le k}(t_j + |a_j - i|), $$ 其中 $|a_j - i|$ 表示 $a_j$ 与 $i$ 的绝对值差。 换句话说，第 $i$ 个格子的温度等于所有空调温度加上它们到第 $i$ 个格子的距离后的最小值。 让我们来看一个例子。假设 $n=6, k=2$，第一台空调放在第 $a_1=2$ 个格子，温度为 $t_1=14$，第二台空调放在第 $a_2=5$ 个格子，温度为 $t_2=16$。此时各格子的温度如下： 1. 第 $1$ 个格子的温度为：$\min(14 + |2 - 1|, 16 + |5 - 1|)=\min(14 + 1, 16 + 4)=\min(15, 20)=15$； 2. 第 $2$ 个格子的温度为：$\min(14 + |2 - 2|, 16 + |5 - 2|)=\min(14 + 0, 16 + 3)=\min(14, 19)=14$； 3. 第 $3$ 个格子的温度为：$\min(14 + |2 - 3|, 16 + |5 - 3|)=\min(14 + 1, 16 + 2)=\min(15, 18)=15$； 4. 第 $4$ 个格子的温度为：$\min(14 + |2 - 4|, 16 + |5 - 4|)=\min(14 + 2, 16 + 1)=\min(16, 17)=16$； 5. 第 $5$ 个格子的温度为：$\min(14 + |2 - 5|, 16 + |5 - 5|)=\min(14 + 3, 16 + 0)=\min(17, 16)=16$； 6. 第 $6$ 个格子的温度为：$\min(14 + |2 - 6|, 16 + |5 - 6|)=\min(14 + 4, 16 + 1)=\min(18, 17)=17$。 请你对于每个格子 $1$ 到 $n$，求出其温度。

第一行包含一个整数 $q$（$1 \le q \le 10^4$），表示测试用例的数量。接下来是 $q$ 组测试用例。每组测试用例前有一个空行。 每组测试用例包含三行。第一行包含两个整数 $n$（$1 \le n \le 3 \times 10^5$）和 $k$（$1 \le k \le n$），分别表示狭长地带的长度和空调的数量。 第二行包含 $k$ 个整数 $a_1, a_2, \ldots, a_k$（$1 \le a_i \le n$），表示空调在狭长地带上的位置。 第三行包含 $k$ 个整数 $t_1, t_2, \ldots, t_k$（$1 \le t_i \le 10^9$），表示空调的温度。 保证所有测试用例中 $n$ 的总和不超过 $3 \times 10^5$。

对于每组测试用例，输出 $n$ 个用空格分隔的整数，表示每个格子的温度。

由 ChatGPT 4.1 翻译