CF1547G How Many Paths?

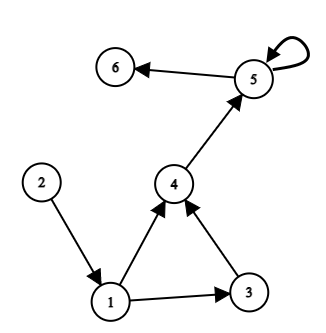
给定一个有向图 $G$，该图可能包含自环（即从某个顶点指向自身的边）。图中不存在重边，即对于所有有序对 $(u, v)$，从 $u$ 到 $v$ 最多只有一条边。顶点编号为 $1$ 到 $n$。 从 $u$ 到 $v$ 的一条路径定义为一系列边，满足： - 顶点 $u$ 是路径中第一条边的起点； - 顶点 $v$ 是路径中最后一条边的终点； - 对于所有相邻的两条边，后一条边的起点等于前一条边的终点。 我们约定，空的边序列也是从 $u$ 到 $u$ 的一条路径。 对于每个顶点 $v$，输出以下四种值之一： - $0$，如果不存在从 $1$ 到 $v$ 的路径； - $1$，如果从 $1$ 到 $v$ 只有一条路径； - $2$，如果从 $1$ 到 $v$ 有多条路径且路径数是有限的； - $-1$，如果从 $1$ 到 $v$ 的路径数是无限的。 请参考下图中的示例：  则： - 顶点 $1$ 的答案为 $1$：只有一条从 $1$ 到 $1$ 的路径（长度为 $0$ 的路径）； - 顶点 $2$ 的答案为 $0$：不存在从 $1$ 到 $2$ 的路径； - 顶点 $3$ 的答案为 $1$：只有一条从 $1$ 到 $3$ 的路径（即边 $(1, 3)$）； - 顶点 $4$ 的答案为 $2$：从 $1$ 到 $4$ 有多条路径且数量有限（两条路径：$[(1, 3), (3, 4)]$ 和 $[(1, 4)]$）； - 顶点 $5$ 的答案为 $-1$：从 $1$ 到 $5$ 的路径数是无限的（可以多次经过环）； - 顶点 $6$ 的答案为 $-1$：从 $1$ 到 $6$ 的路径数是无限的（可以多次经过环）。

第一行为一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。接下来是 $t$ 组测试用例。每组测试用例前有一个空行。 每组测试用例的第一行为两个整数 $n$ 和 $m$（$1 \le n \le 4 \cdot 10^5, 0 \le m \le 4 \cdot 10^5$），分别表示图的顶点数和边数。接下来的 $m$ 行，每行包含两个整数 $a_i$ 和 $b_i$（$1 \le a_i, b_i \le n$），表示第 $i$ 条边的起点和终点。顶点编号为 $1$ 到 $n$。图中可能存在自环（即 $a_i = b_i$），但不存在重边（即不存在 $a_i = a_j$ 且 $b_i = b_j$ 且 $i \ne j$）。 所有测试用例中 $n$ 的总和不超过 $4 \cdot 10^5$，$m$ 的总和也不超过 $4 \cdot 10^5$。

输出 $t$ 行，第 $i$ 行为第 $i$ 个测试用例的答案：$n$ 个整数，分别为 $-1$ 到 $2$ 之间的值。

由 ChatGPT 4.1 翻译