CF1547G How Many Paths?

You are given a directed graph $ G $ which can contain loops (edges from a vertex to itself). Multi-edges are absent in $ G $ which means that for all ordered pairs $ (u, v) $ exists at most one edge from $ u $ to $ v $ . Vertices are numbered from $ 1 $ to $ n $ . A path from $ u $ to $ v $ is a sequence of edges such that: - vertex $ u $ is the start of the first edge in the path; - vertex $ v $ is the end of the last edge in the path; - for all pairs of adjacent edges next edge starts at the vertex that the previous edge ends on. We will assume that the empty sequence of edges is a path from $ u $ to $ u $ . For each vertex $ v $ output one of four values: - $ 0 $ , if there are no paths from $ 1 $ to $ v $ ; - $ 1 $ , if there is only one path from $ 1 $ to $ v $ ; - $ 2 $ , if there is more than one path from $ 1 $ to $ v $ and the number of paths is finite; - $ -1 $ , if the number of paths from $ 1 $ to $ v $ is infinite. Let's look at the example shown in the figure. 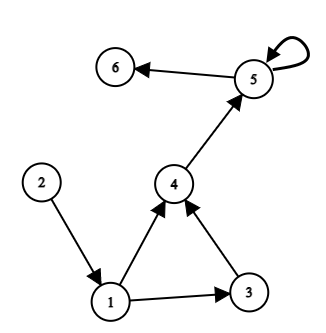Then: - the answer for vertex $ 1 $ is $ 1 $ : there is only one path from $ 1 $ to $ 1 $ (path with length $ 0 $ ); - the answer for vertex $ 2 $ is $ 0 $ : there are no paths from $ 1 $ to $ 2 $ ; - the answer for vertex $ 3 $ is $ 1 $ : there is only one path from $ 1 $ to $ 3 $ (it is the edge $ (1, 3) $ ); - the answer for vertex $ 4 $ is $ 2 $ : there are more than one paths from $ 1 $ to $ 4 $ and the number of paths are finite (two paths: $ [(1, 3), (3, 4)] $ and $ [(1, 4)] $ ); - the answer for vertex $ 5 $ is $ -1 $ : the number of paths from $ 1 $ to $ 5 $ is infinite (the loop can be used in a path many times); - the answer for vertex $ 6 $ is $ -1 $ : the number of paths from $ 1 $ to $ 6 $ is infinite (the loop can be used in a path many times).

The first contains an integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases in the input. Then $ t $ test cases follow. Before each test case, there is an empty line. The first line of the test case contains two integers $ n $ and $ m $ ( $ 1 \le n \le 4 \cdot 10^5, 0 \le m \le 4 \cdot 10^5 $ ) — numbers of vertices and edges in graph respectively. The next $ m $ lines contain edges descriptions. Each line contains two integers $ a_i $ , $ b_i $ ( $ 1 \le a_i, b_i \le n $ ) — the start and the end of the $ i $ -th edge. The vertices of the graph are numbered from $ 1 $ to $ n $ . The given graph can contain loops (it is possible that $ a_i = b_i $ ), but cannot contain multi-edges (it is not possible that $ a_i = a_j $ and $ b_i = b_j $ for $ i \ne j $ ). The sum of $ n $ over all test cases does not exceed $ 4 \cdot 10^5 $ . Similarly, the sum of $ m $ over all test cases does not exceed $ 4 \cdot 10^5 $ .

Output $ t $ lines. The $ i $ -th line should contain an answer for the $ i $ -th test case: a sequence of $ n $ integers from $ -1 $ to $ 2 $ .