CF1548A Web of Lies

当你玩权力的游戏时，你要么赢，要么死。没有中间地带。 ——瑟曦·兰尼斯特，《权力的游戏》，乔治·R·R·马丁 有 $n$ 位贵族，编号从 $1$ 到 $n$。第 $i$ 位贵族的权力值为 $i$。还有 $m$ 对“友谊”关系。贵族 $a$ 和 $b$ 之间的友谊总是互相的。 如果满足以下两个条件，则称某位贵族是“脆弱的”： - 该贵族至少有一位朋友，并且 - 该贵族所有的朋友权力值都比他高。 你需要处理以下三种类型的操作： 1. 在贵族 $u$ 和 $v$ 之间添加一段友谊。 2. 在贵族 $u$ 和 $v$ 之间移除一段友谊。 3. 计算如下过程的结果。 过程如下：所有脆弱的贵族会被同时杀死，并且他们的所有友谊关系都会消失。然后，可能会有新的贵族变得脆弱。这个过程会不断重复，直到没有脆弱的贵族为止。可以证明，这个过程一定会在有限步内结束。过程结束后，你需要计算剩下的贵族数量。 注意，每次第 3 类操作时，过程都是从所有贵族都存活的状态开始的，前一次操作的结果不会影响后续操作！

第一行包含两个整数 $n$ 和 $m$（$1 \le n \le 2 \cdot 10^5$，$0 \le m \le 2 \cdot 10^5$），分别表示贵族的数量和初始友谊的数量。 接下来的 $m$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \ne v$），表示一对友谊关系。不会有重复的友谊关系。 接下来一行包含一个整数 $q$（$1 \le q \le 2 \cdot 10^5$），表示操作的数量。 接下来的 $q$ 行，每行表示一个操作，格式如下： - $1\ u\ v$（$1 \le u, v \le n$，$u \ne v$）：在 $u$ 和 $v$ 之间添加一段友谊。保证此时 $u$ 和 $v$ 不是朋友。 - $2\ u\ v$（$1 \le u, v \le n$，$u \ne v$）：在 $u$ 和 $v$ 之间移除一段友谊。保证此时 $u$ 和 $v$ 是朋友。 - $3$：输出当前过程结束后剩余贵族的数量。 保证至少有一次第 3 类操作。

对于每个第 3 类操作，输出一个整数，表示过程结束后剩余的贵族数量，每个答案占一行。

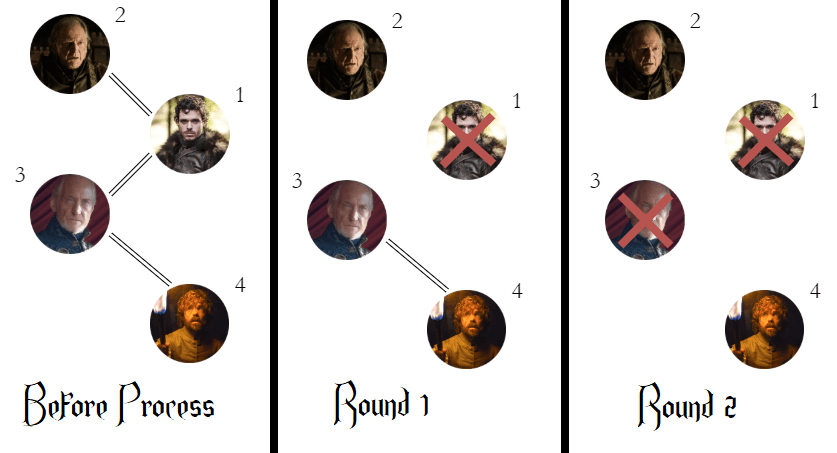
考虑第一个样例。在第一次第 3 类操作时，关系图如下： 在过程的第一轮，贵族 $1$ 的所有朋友（$2$ 和 $3$）权力值都比他高，因此 $1$ 被杀死。第一轮没有其他贵族脆弱。第二轮，贵族 $3$ 仅剩的朋友是 $4$，权力值比他高，因此 $3$ 被杀死。此时过程结束，答案为 $2$。  在第二次第 3 类操作时，唯一存活的贵族是 $4$。 第二个样例只有一次第 3 类操作。第一轮有两位贵族被杀死，第二轮又有一位被杀死。最终只剩下 $1$ 位贵族存活。  由 ChatGPT 4.1 翻译