CF1548D2 Gregor and the Odd Cows (Hard)
题目描述
这是该问题的困难版本。与简单版本的唯一区别在于,本版本中坐标既可以是奇数也可以是偶数。
平面上有 $n$ 个栅栏柱,且它们的坐标各不相同。保证没有三根栅栏柱共线。
在平面上的每一个整点坐标处都有一头奶牛,也就是说,平面上所有整数坐标点上都存在奶牛。
Gregor 是光明会的一员,他想要用三根不同的现有栅栏柱连接起来,建造一个三角形的围栏。如果一头奶牛严格在围栏内部,则称其被围住。如果被围住的奶牛数量为奇数,并且围栏的面积为整数,则称该围栏是有趣的。
请你求出有趣的围栏的数量。
输入格式
第一行包含一个整数 $n$($3 \le n \le 6000$),表示 Gregor 可以选择作为围栏顶点的栅栏柱数量。
接下来的 $n$ 行,每行包含两个整数 $x$ 和 $y$($0 \le x, y \le 10^7$),表示一个栅栏柱的坐标。所有栅栏柱的坐标均不相同,且没有三根栅栏柱共线。
输出格式
输出一个整数,表示有趣的围栏的数量。如果用不同的三根栅栏柱建造的围栏被认为是不同的。
说明/提示
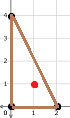
在第一个样例中,只有 $1$ 个围栏。该围栏是有趣的,因为它的面积为 $4$,且被围住的奶牛数量为 $1$,如图中红色所示。
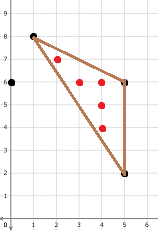
在第二个样例中,共有 $4$ 种可能的围栏,但只有其中一个是有趣的。该围栏的面积为 $8$,且被围住的奶牛数量为 $5$。
由 ChatGPT 4.1 翻译