CF1548E Gregor and the Two Painters

Two painters, Amin and Benj, are repainting Gregor's living room ceiling! The ceiling can be modeled as an $ n \times m $ grid. For each $ i $ between $ 1 $ and $ n $ , inclusive, painter Amin applies $ a_i $ layers of paint to the entire $ i $ -th row. For each $ j $ between $ 1 $ and $ m $ , inclusive, painter Benj applies $ b_j $ layers of paint to the entire $ j $ -th column. Therefore, the cell $ (i,j) $ ends up with $ a_i+b_j $ layers of paint. Gregor considers the cell $ (i,j) $ to be badly painted if $ a_i+b_j \le x $ . Define a badly painted region to be a maximal connected component of badly painted cells, i. e. a connected component of badly painted cells such that all adjacent to the component cells are not badly painted. Two cells are considered adjacent if they share a side. Gregor is appalled by the state of the finished ceiling, and wants to know the number of badly painted regions.

The first line contains three integers $ n $ , $ m $ and $ x $ ( $ 1 \le n,m \le 2\cdot 10^5 $ , $ 1 \le x \le 2\cdot 10^5 $ ) — the dimensions of Gregor's ceiling, and the maximum number of paint layers in a badly painted cell. The second line contains $ n $ integers $ a_1, a_2, \ldots, a_n $ ( $ 1 \le a_i \le 2\cdot 10^5 $ ), the number of paint layers Amin applies to each row. The third line contains $ m $ integers $ b_1, b_2, \ldots, b_m $ ( $ 1 \le b_j \le 2\cdot 10^5 $ ), the number of paint layers Benj applies to each column.

Print a single integer, the number of badly painted regions.

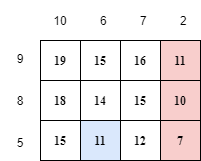
The diagram below represents the first example. The numbers to the left of each row represent the list $ a $ , and the numbers above each column represent the list $ b $ . The numbers inside each cell represent the number of paint layers in that cell. The colored cells correspond to badly painted cells. The red and blue cells respectively form $ 2 $ badly painted regions.