CF1552C Maximize the Intersections
题目描述
在一个圆上有 $2n$ 个不同的点,满足如下性质:无论你选择 $3$ 条连接 $3$ 对不相交点的弦,都不存在一个严格在圆内部的点同时属于这 $3$ 条弦。点按顺时针顺序编号为 $1,\,2,\,\dots,\,2n$。
最初,有 $k$ 条弦连接了 $k$ 对点,且这 $2k$ 个端点两两不同。
你需要再画出 $n-k$ 条弦,将剩下的 $2(n-k)$ 个点两两配对(每个点恰好作为一条弦的端点)。
最终,设 $x$ 为所有 $n$ 条弦之间的交点总数。请计算在最优选择 $n-k$ 条新弦的情况下,$x$ 的最大值。
注意,$2n$ 个点的具体位置无关紧要,只要满足第一段描述的性质即可。
输入格式
第一行包含一个整数 $t$($1 \le t \le 100$),表示测试用例的数量。接下来有 $t$ 组测试数据。
每组测试数据的第一行包含两个整数 $n$ 和 $k$($1 \le n \le 100$,$0 \le k \le n$),分别表示点对数和初始已画的弦数。
接下来的 $k$ 行,每行包含两个整数 $x_i$ 和 $y_i$($1 \le x_i,\,y_i \le 2n$,$x_i \ne y_i$),表示第 $i$ 条弦的两个端点。保证所有 $2k$ 个端点都互不相同。
输出格式
对于每个测试用例,输出通过最优选择 $n-k$ 条新弦所能获得的最大交点数。
说明/提示
在第一个测试用例中,有三种方式画出 $2$ 条新弦,如下图所示(黑色为初始弦,红色为新弦):
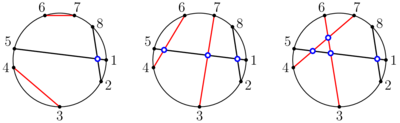
可以看到第三种方式获得的交点数最多,为 $4$。
在第二个测试用例中,没有更多弦可画。显然,只有一条弦时没有交点。
在第三个测试用例中,可以通过画 $1-3$ 和 $2-4$ 两条弦获得最多 $1$ 个交点,如下图所示:
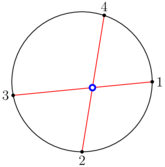
由 ChatGPT 4.1 翻译