CF1552E Colors and Intervals

将 $1,\,2,\,\dots,\,n \cdot k$ 这 $n \cdot k$ 个数用 $n$ 种颜色进行染色。这些颜色编号为 $1,\,2,\,\dots,\,n$。对于每个 $1 \le i \le n$，恰好有 $k$ 个数被染成颜色 $i$。 设 $[a,\,b]$ 表示区间 $a$ 到 $b$ 的所有整数，即集合 $\{a,\,a+1,\,\dots,\,b\}$。你需要选择 $n$ 个区间 $[a_1,\,b_1],\,[a_2,\,b_2],\,\dots,[a_n,\,b_n]$，使得： - 对于每个 $1 \le i \le n$，有 $1 \le a_i < b_i \le n \cdot k$； - 对于每个 $1 \le i \le n$，数 $a_i$ 和 $b_i$ 都被染成颜色 $i$； - 每个 $1 \le x \le n \cdot k$ 的数最多只属于 $\left\lceil \frac{n}{k - 1} \right\rceil$ 个区间。 可以证明，在给定的限制条件下，总能找到满足要求的区间集合。

第一行包含两个整数 $n$ 和 $k$（$1 \le n \le 100$，$2 \le k \le 100$），分别表示颜色的数量和每种颜色出现的次数。 第二行包含 $n \cdot k$ 个整数 $c_1,\,c_2,\,\dots,\,c_{nk}$（$1 \le c_j \le n$），其中 $c_j$ 表示数字 $j$ 的颜色。保证对于每个 $1 \le i \le n$，恰好有 $k$ 个不同的 $j$ 满足 $c_j = i$。

输出 $n$ 行。第 $i$ 行输出两个整数 $a_i$ 和 $b_i$。 如果存在多组合法的区间，输出任意一组均可。

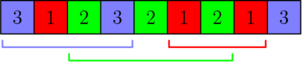
在第一个样例中，每个数字最多可以被包含在 $\left\lceil \frac{4}{3 - 1} \right\rceil = 2$ 个区间中。输出可以用下图表示：  在第二个样例中，唯一可选的区间只能是 $[1,\,2]$，每个数字确实最多只被包含在 $\left\lceil \frac{1}{2 - 1} \right\rceil = 1$ 个区间中。 在第三个样例中，每个数字最多可以被包含在 $\left\lceil \frac{3}{3 - 1} \right\rceil = 2$ 个区间中。输出可以用下图表示：  由 ChatGPT 4.1 翻译