CF1552E Colors and Intervals

The numbers $ 1, \, 2, \, \dots, \, n \cdot k $ are colored with $ n $ colors. These colors are indexed by $ 1, \, 2, \, \dots, \, n $ . For each $ 1 \le i \le n $ , there are exactly $ k $ numbers colored with color $ i $ . Let $ [a, \, b] $ denote the interval of integers between $ a $ and $ b $ inclusive, that is, the set $ \{a, \, a + 1, \, \dots, \, b\} $ . You must choose $ n $ intervals $ [a_1, \, b_1], \, [a_2, \, b_2], \, \dots, [a_n, \, b_n] $ such that: - for each $ 1 \le i \le n $ , it holds $ 1 \le a_i < b_i \le n \cdot k $ ; - for each $ 1 \le i \le n $ , the numbers $ a_i $ and $ b_i $ are colored with color $ i $ ; - each number $ 1 \le x \le n \cdot k $ belongs to at most $ \left\lceil \frac{n}{k - 1} \right\rceil $ intervals. One can show that such a family of intervals always exists under the given constraints.

The first line contains two integers $ n $ and $ k $ ( $ 1 \le n \le 100 $ , $ 2 \le k \le 100 $ ) — the number of colors and the number of occurrences of each color. The second line contains $ n \cdot k $ integers $ c_1, \, c_2, \, \dots, \, c_{nk} $ ( $ 1 \le c_j \le n $ ), where $ c_j $ is the color of number $ j $ . It is guaranteed that, for each $ 1 \le i \le n $ , it holds $ c_j = i $ for exactly $ k $ distinct indices $ j $ .

Output $ n $ lines. The $ i $ -th line should contain the two integers $ a_i $ and $ b_i $ . If there are multiple valid choices of the intervals, output any.

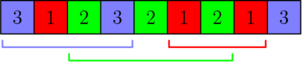
In the first sample, each number can be contained in at most $ \left\lceil \frac{4}{3 - 1} \right\rceil = 2 $ intervals. The output is described by the following picture: In the second sample, the only interval to be chosen is forced to be $ [1, \, 2] $ , and each number is indeed contained in at most $ \left\lceil \frac{1}{2 - 1} \right\rceil = 1 $ interval. In the third sample, each number can be contained in at most $ \left\lceil \frac{3}{3 - 1} \right\rceil = 2 $ intervals. The output is described by the following picture: