CF1554E You

You are given a tree with $ n $ nodes. As a reminder, a tree is a connected undirected graph without cycles. Let $ a_1, a_2, \ldots, a_n $ be a sequence of integers. Perform the following operation exactly $ n $ times: - Select an unerased node $ u $ . Assign $ a_u := $ number of unerased nodes adjacent to $ u $ . Then, erase the node $ u $ along with all edges that have it as an endpoint. For each integer $ k $ from $ 1 $ to $ n $ , find the number, modulo $ 998\,244\,353 $ , of different sequences $ a_1, a_2, \ldots, a_n $ that satisfy the following conditions: - it is possible to obtain $ a $ by performing the aforementioned operations exactly $ n $ times in some order. - $ \operatorname{gcd}(a_1, a_2, \ldots, a_n) = k $ . Here, $ \operatorname{gcd} $ means the greatest common divisor of the elements in $ a $ .

The first line contains a single integer $ t $ ( $ 1 \le t \le 10\,000 $ ) — the number of test cases. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 10^5 $ ). Each of the next $ n - 1 $ lines contains two integers $ u $ and $ v $ ( $ 1 \le u, v \le n $ ) indicating there is an edge between vertices $ u $ and $ v $ . It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases doesn't exceed $ 3 \cdot 10^5 $ .

For each test case, print $ n $ integers in a single line, where for each $ k $ from $ 1 $ to $ n $ , the $ k $ -th integer denotes the answer when $ \operatorname{gcd} $ equals to $ k $ .

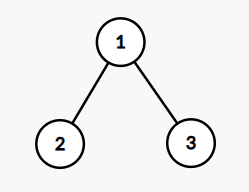In the first test case, - If we delete the nodes in order $ 1 \rightarrow 2 \rightarrow 3 $ or $ 1 \rightarrow 3 \rightarrow 2 $ , then the obtained sequence will be $ a = [2, 0, 0] $ which has $ \operatorname{gcd} $ equals to $ 2 $ . - If we delete the nodes in order $ 2 \rightarrow 1 \rightarrow 3 $ , then the obtained sequence will be $ a = [1, 1, 0] $ which has $ \operatorname{gcd} $ equals to $ 1 $ . - If we delete the nodes in order $ 3 \rightarrow 1 \rightarrow 2 $ , then the obtained sequence will be $ a = [1, 0, 1] $ which has $ \operatorname{gcd} $ equals to $ 1 $ . - If we delete the nodes in order $ 2 \rightarrow 3 \rightarrow 1 $ or $ 3 \rightarrow 2 \rightarrow 1 $ , then the obtained sequence will be $ a = [0, 1, 1] $ which has $ \operatorname{gcd} $ equals to $ 1 $ . Note that here we are counting the number of different sequences, not the number of different orders of deleting nodes.