CF1556F Sports Betting

William 不仅对交易感兴趣，还喜欢对体育比赛进行投注。有 $n$ 支队伍参加每场比赛。每支队伍有一个实力值 $a_i$。每两支队伍 $i < j$ 恰好互相比赛一次。队伍 $i$ 获胜的概率为 $\frac{a_i}{a_i + a_j}$，队伍 $j$ 获胜的概率为 $\frac{a_j}{a_i + a_j}$。 如果一支队伍直接或间接击败了所有其他队伍，则称其为“胜者”。如果存在一系列队伍 $c_1, c_2, \dots, c_k$，使得 $c_1 = a$，$c_k = b$，并且对于所有 $i$ 从 $1$ 到 $k-1$，队伍 $c_i$ 击败了队伍 $c_{i+1}$，则称队伍 $a$ 直接或间接击败了队伍 $b$。注意，可能出现队伍 $a$ 击败了队伍 $b$，同时队伍 $b$ 也击败了队伍 $a$ 的情况。 William 想让你求出本次比赛中胜者数量的期望值。

第一行包含一个整数 $n$（$1 \leq n \leq 14$），表示参加比赛的队伍总数。 第二行包含 $n$ 个整数 $a_1, a_2, \dots, a_n$（$1 \leq a_i \leq 10^6$），表示每支队伍的实力值。

输出一个整数，表示本次比赛中胜者数量的期望值，结果对 $10^9 + 7$ 取模。 形式化地，设 $M = 10^9+7$。可以证明答案可以表示为最简分数 $\frac{p}{q}$，其中 $p$ 和 $q$ 是整数，且 $q \not\equiv 0 \pmod{M}$。请输出一个整数 $x$，满足 $0 \le x < M$ 且 $x \cdot q \equiv p \pmod{M}$。

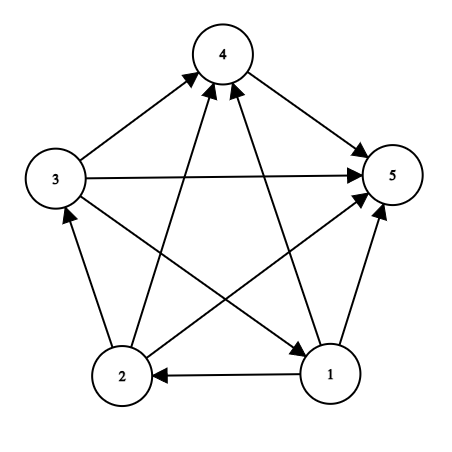
为了更好地理解在什么情况下可能有多个胜者，让我们来看第二个测试样例： 比赛的一种可能结果如下（$a \rightarrow b$ 表示 $a$ 击败了 $b$）： - $1 \rightarrow 2$ - $2 \rightarrow 3$ - $3 \rightarrow 1$ - $1 \rightarrow 4$ - $1 \rightarrow 5$ - $2 \rightarrow 4$ - $2 \rightarrow 5$ - $3 \rightarrow 4$ - $3 \rightarrow 5$ - $4 \rightarrow 5$ 更直观地用图表示：  在这种情况下，集合 $\{1, 2, 3\}$ 中的每支队伍都直接或间接击败了所有人。即： - 第 $1$ 支队伍击败了所有人，因为可以通过 $1 \rightarrow 2$，$1 \rightarrow 2 \rightarrow 3$，$1 \rightarrow 4$，$1 \rightarrow 5$ 到达其他所有队伍。 - 第 $2$ 支队伍击败了所有人，因为可以通过 $2 \rightarrow 3$，$2 \rightarrow 3 \rightarrow 1$，$2 \rightarrow 4$，$2 \rightarrow 5$ 到达其他所有队伍。 - 第 $3$ 支队伍击败了所有人，因为可以通过 $3 \rightarrow 1$，$3 \rightarrow 1 \rightarrow 2$，$3 \rightarrow 4$，$3 \rightarrow 5$ 到达其他所有队伍。 因此，胜者的总数为 $3$。 由 ChatGPT 4.1 翻译