CF1556G Gates to Another World

As mentioned previously William really likes playing video games. In one of his favorite games, the player character is in a universe where every planet is designated by a binary number from $ 0 $ to $ 2^n - 1 $ . On each planet, there are gates that allow the player to move from planet $ i $ to planet $ j $ if the binary representations of $ i $ and $ j $ differ in exactly one bit. William wants to test you and see how you can handle processing the following queries in this game universe: - Destroy planets with numbers from $ l $ to $ r $ inclusively. These planets cannot be moved to anymore. - Figure out if it is possible to reach planet $ b $ from planet $ a $ using some number of planetary gates. It is guaranteed that the planets $ a $ and $ b $ are not destroyed.

The first line contains two integers $ n $ , $ m $ ( $ 1 \leq n \leq 50 $ , $ 1 \leq m \leq 5 \cdot 10^4 $ ), which are the number of bits in binary representation of each planets' designation and the number of queries, respectively. Each of the next $ m $ lines contains a query of two types: block l r — query for destruction of planets with numbers from $ l $ to $ r $ inclusively ( $ 0 \le l \le r < 2^n $ ). It's guaranteed that no planet will be destroyed twice. ask a b — query for reachability between planets $ a $ and $ b $ ( $ 0 \le a, b < 2^n $ ). It's guaranteed that planets $ a $ and $ b $ hasn't been destroyed yet.

For each query of type ask you must output "1" in a new line, if it is possible to reach planet $ b $ from planet $ a $ and "0" otherwise (without quotation marks).

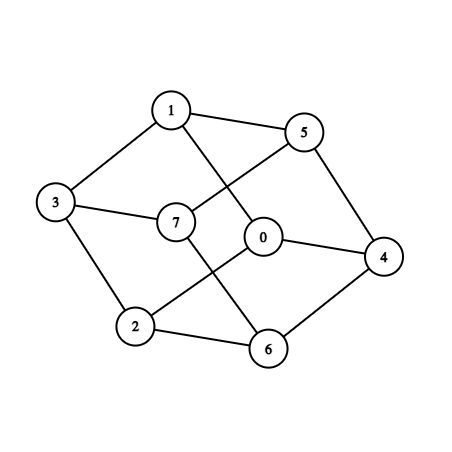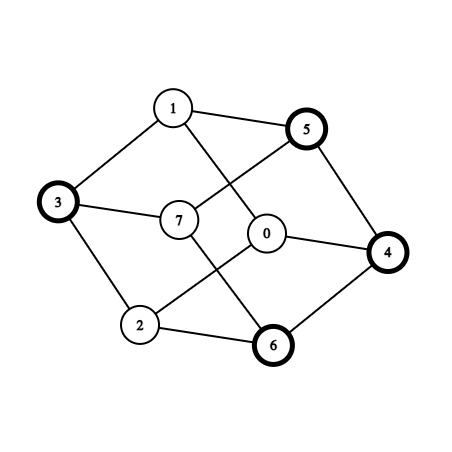The first example test can be visualized in the following way: Response to a query ask 0 7 is positive. Next after query block 3 6 the graph will look the following way (destroyed vertices are highlighted): Response to a query ask 0 7 is negative, since any path from vertex $ 0 $ to vertex $ 7 $ must go through one of the destroyed vertices.