CF1566E Buds Re-hanging

一棵树是一个无环连通图。有根树有一个特殊的顶点，称为根。顶点 $v$（不同于根）的父亲是从根到顶点 $v$ 的最短路径上的前一个顶点。顶点 $v$ 的子节点是所有以 $v$ 为父亲的顶点。 如果一个顶点没有子节点，则称其为叶子。我们称一个顶点为“芽”，如果满足以下三个条件： - 它不是根节点； - 它至少有一个子节点； - 它的所有子节点都是叶子。 给定一棵有 $n$ 个顶点的有根树，顶点 $1$ 是根。在一次操作中，你可以选择任意一个“芽”及其所有子节点（这些子节点都是叶子），并将它们挂到树中的任意其他顶点下。这样做时，你会删除连接“芽”与其父节点的边，并添加一条“芽”与所选顶点之间的边。所选顶点不能是该“芽”自身或其任何子节点。所有“芽”的子节点仍然与“芽”相连。 你可以进行任意次数上述操作（也可以不操作）。请问，经过若干次操作后，树中最少能有多少个叶子？

输入包含多组测试数据。第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 2 \cdot 10^5$），表示树中顶点的数量。 接下来的 $n-1$ 行，每行包含两个整数 $u$ 和 $v$（$1 \le u, v \le n$，$u \neq v$），表示树中存在一条连接顶点 $u$ 和 $v$ 的边。 保证给定的图是一棵树。 保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示经过若干次操作后树中可能得到的最少叶子数。

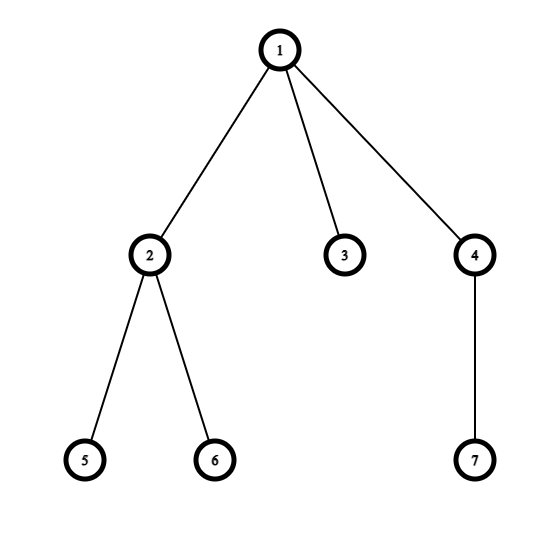
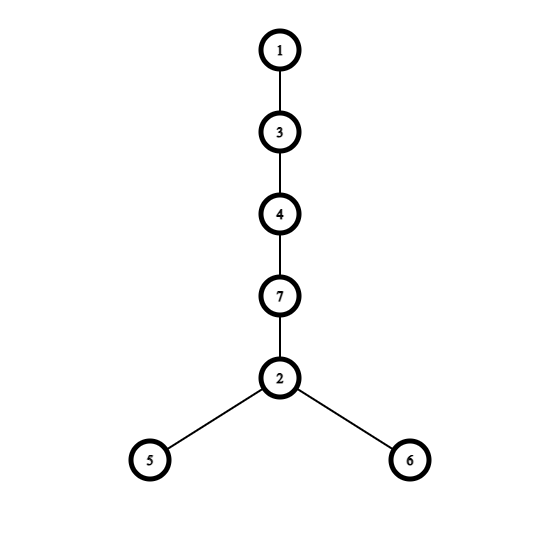
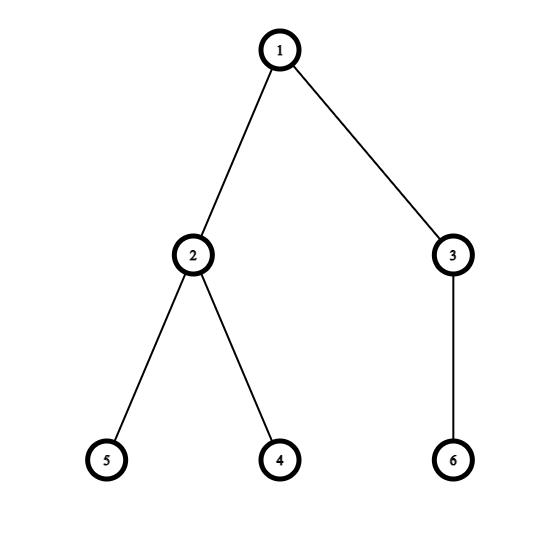
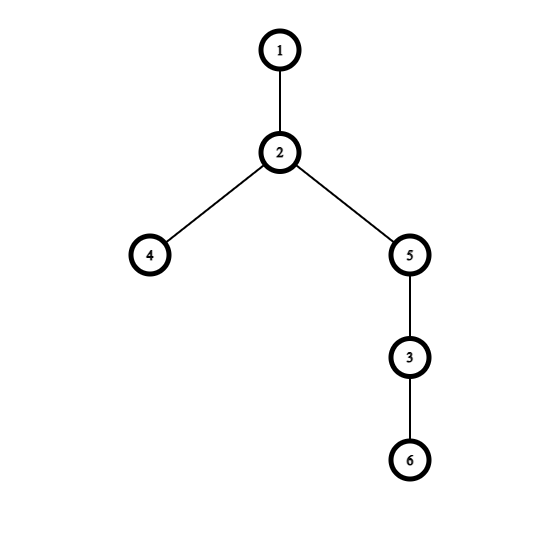
在第一个测试用例中，树的结构如下：  首先，你可以选择“芽”顶点 $4$ 并将其挂到顶点 $3$ 下。之后，你可以选择“芽”顶点 $2$ 并将其挂到顶点 $7$ 下。最终，你将得到如下结构的树，有 $2$ 个叶子：  可以证明，这就是可能得到的最少叶子数。 在第二个测试用例中，树的结构如下：  你可以选择“芽”顶点 $3$ 并将其挂到顶点 $5$ 下。最终，你将得到如下结构的树，有 $2$ 个叶子：  可以证明，这就是可能得到的最少叶子数。 由 ChatGPT 4.1 翻译