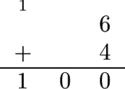CF1567C Carrying Conundrum

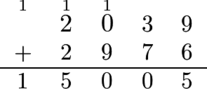Alice has just learned addition. However, she hasn't learned the concept of "carrying" fully — instead of carrying to the next column, she carries to the column two columns to the left. For example, the regular way to evaluate the sum $ 2039 + 2976 $ would be as shown: However, Alice evaluates it as shown: In particular, this is what she does: - add $ 9 $ and $ 6 $ to make $ 15 $ , and carry the $ 1 $ to the column two columns to the left, i. e. to the column " $ 0 $ $ 9 $ "; - add $ 3 $ and $ 7 $ to make $ 10 $ and carry the $ 1 $ to the column two columns to the left, i. e. to the column " $ 2 $ $ 2 $ "; - add $ 1 $ , $ 0 $ , and $ 9 $ to make $ 10 $ and carry the $ 1 $ to the column two columns to the left, i. e. to the column above the plus sign; - add $ 1 $ , $ 2 $ and $ 2 $ to make $ 5 $ ; - add $ 1 $ to make $ 1 $ . Thus, she ends up with the incorrect result of $ 15005 $ .Alice comes up to Bob and says that she has added two numbers to get a result of $ n $ . However, Bob knows that Alice adds in her own way. Help Bob find the number of ordered pairs of positive integers such that when Alice adds them, she will get a result of $ n $ . Note that pairs $ (a, b) $ and $ (b, a) $ are considered different if $ a \ne b $ .

The input consists of multiple test cases. The first line contains an integer $ t $ ( $ 1 \leq t \leq 1000 $ ) — the number of test cases. The description of the test cases follows. The only line of each test case contains an integer $ n $ ( $ 2 \leq n \leq 10^9 $ ) — the number Alice shows Bob.

For each test case, output one integer — the number of ordered pairs of positive integers such that when Alice adds them, she will get a result of $ n $ .

In the first test case, when Alice evaluates any of the sums $ 1 + 9 $ , $ 2 + 8 $ , $ 3 + 7 $ , $ 4 + 6 $ , $ 5 + 5 $ , $ 6 + 4 $ , $ 7 + 3 $ , $ 8 + 2 $ , or $ 9 + 1 $ , she will get a result of $ 100 $ . The picture below shows how Alice evaluates $ 6 + 4 $ :