CF1567C Carrying Conundrum
题目描述
Alice 刚学会加法。然而,她还没有完全理解“进位”的概念——她不是向左一位进位,而是向左两位进位。
例如,正常情况下计算 $2039 + 2976$ 的过程如下:

然而,Alice 的计算方式如下:
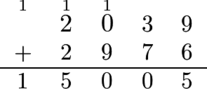
具体来说,她的做法如下:
- 将 $9$ 和 $6$ 相加得到 $15$,并把 $1$ 进位到左边第二列,也就是“$0$ $9$”那一列;
- 将 $3$ 和 $7$ 相加得到 $10$,并把 $1$ 进位到左边第二列,也就是“$2$ $2$”那一列;
- 将 $1$、$0$ 和 $9$ 相加得到 $10$,并把 $1$ 进位到左边第二列,也就是加号上方那一列;
- 将 $1$、$2$ 和 $2$ 相加得到 $5$;
- 将 $1$ 单独写下得到 $1$。
因此,她最终得到了错误的结果 $15005$。
现在,Alice 走到 Bob 面前,说她将两个数相加得到了 $n$。但 Bob 知道 Alice 是用她自己的方式加的。请你帮助 Bob 计算,有多少对有序正整数对 $(a, b)$,使得 Alice 用她的方式相加后结果为 $n$。注意,如果 $a \ne b$,则 $(a, b)$ 和 $(b, a)$ 被视为不同的有序对。
输入格式
输入包含多组测试用例。第一行包含一个整数 $t$($1 \leq t \leq 1000$),表示测试用例的数量。
接下来每个测试用例一行,包含一个整数 $n$($2 \leq n \leq 10^9$),表示 Alice 展示给 Bob 的结果。
输出格式
对于每个测试用例,输出一个整数,表示有多少对有序正整数对 $(a, b)$,使得 Alice 用她的方式相加后结果为 $n$。
说明/提示
在第一个测试用例中,无论 Alice 计算 $1 + 9$、$2 + 8$、$3 + 7$、$4 + 6$、$5 + 5$、$6 + 4$、$7 + 3$、$8 + 2$ 或 $9 + 1$,她都会得到 $100$。下图展示了 Alice 计算 $6 + 4$ 的过程:
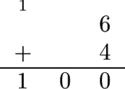
由 ChatGPT 4.1 翻译