CF1569D Inconvenient Pairs

有一座城市可以表示为一个正方形网格，其顶点坐标为 $(0, 0)$ 和 $(10^6, 10^6)$。 城市中有 $n$ 条纵向街道和 $m$ 条横向街道，这些街道贯穿整个城市。第 $i$ 条纵向街道从 $(x_i, 0)$ 延伸到 $(x_i, 10^6)$，第 $j$ 条横向街道从 $(0, y_j)$ 延伸到 $(10^6, y_j)$。 所有街道都是双向的。城市的边界也算作街道。 有 $k$ 个人站在街道上：第 $p$ 个人位于点 $(x_p, y_p)$（即 $x_p$ 等于某个 $x_i$ 或 $y_p$ 等于某个 $y_j$，或两者都等于）。 如果两个人之间仅沿街道行走的最短路径严格大于他们之间的曼哈顿距离，则称这两个人构成一个“不便对”。 请计算有多少对不便对（即 $(x, y)$ 和 $(y, x)$ 视为同一对）。 曼哈顿距离定义为：对于点 $(x_1, y_1)$ 和 $(x_2, y_2)$，其曼哈顿距离为 $|x_1 - x_2| + |y_1 - y_2|$。

第一行包含一个整数 $t$（$1 \le t \le 1000$），表示测试用例的数量。 每个测试用例的第一行包含三个整数 $n$、$m$ 和 $k$（$2 \le n, m \le 2 \times 10^5$；$2 \le k \le 3 \times 10^5$），分别表示纵向街道数、横向街道数和人数。 每个测试用例的第二行包含 $n$ 个整数 $x_1, x_2, \dots, x_n$（$0 = x_1 < x_2 < \dots < x_{n-1} < x_n = 10^6$），表示纵向街道的 $x$ 坐标。 第三行包含 $m$ 个整数 $y_1, y_2, \dots, y_m$（$0 = y_1 < y_2 < \dots < y_{m-1} < y_m = 10^6$），表示横向街道的 $y$ 坐标。 接下来的 $k$ 行，每行包含两个整数 $x_p$ 和 $y_p$（$0 \le x_p, y_p \le 10^6$；$x_p \in \{x_1, \dots, x_n\}$ 或 $y_p \in \{y_1, \dots, y_m\}$），表示第 $p$ 个人的位置。所有点均不相同。 保证所有测试用例中 $n$ 的总和不超过 $2 \times 10^5$，$m$ 的总和不超过 $2 \times 10^5$，$k$ 的总和不超过 $3 \times 10^5$。

对于每个测试用例，输出一个整数，表示不便对的数量。

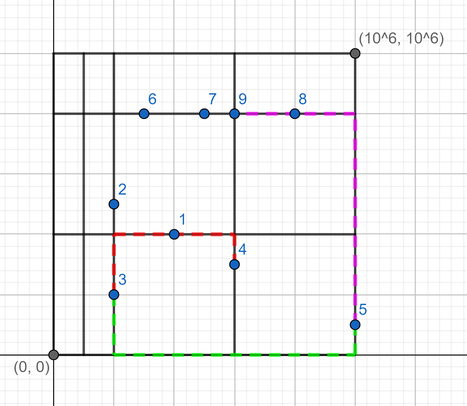
第二个测试用例如图所示：  例如，点 $3$ 和点 $4$ 构成一个不便对，因为它们之间仅沿街道行走的最短路径（红色，长度为 $7$）大于它们的曼哈顿距离（为 $5$）。 点 $3$ 和点 $5$ 也构成一个不便对：最短路径为 $1000001$（绿色），大于曼哈顿距离 $999999$。 但点 $5$ 和点 $9$ 不构成不便对，因为它们之间的最短路径（紫色）等于曼哈顿距离。 由 ChatGPT 4.1 翻译