CF1569E Playoff Restoration

有 $2^k$ 支队伍参加一场淘汰赛。比赛共进行 $2^k - 1$ 场。比赛规则如下：首先，所有队伍被两两分组：第 $1$ 队对阵第 $2$ 队，第 $3$ 队对阵第 $4$ 队（顺序固定），以此类推（因此本轮共进行 $2^{k-1}$ 场比赛）。每场比赛的败者被淘汰，每场比赛都会淘汰一支队伍（没有平局）。之后，剩下 $2^{k-1}$ 支队伍。如果只剩下一支队伍，则该队伍成为冠军；否则，继续进行 $2^{k-2}$ 场比赛：在这些比赛中，第一场由“第 $1$ 队 vs 第 $2$ 队”的胜者对阵“第 $3$ 队 vs 第 $4$ 队”的胜者，第二场由“第 $5$ 队 vs 第 $6$ 队”的胜者对阵“第 $7$ 队 vs 第 $8$ 队”的胜者，依此类推。如此反复，直到只剩下一支队伍。 比赛结束后，队伍根据被淘汰的轮次分配名次，具体如下： - 冠军获得第 $1$ 名； - 决赛被淘汰的队伍获得第 $2$ 名； - 两支在半决赛被淘汰的队伍获得第 $3$ 名； - 所有在四分之一决赛被淘汰的队伍获得第 $5$ 名； - 所有在八分之一决赛被淘汰的队伍获得第 $9$ 名，依此类推。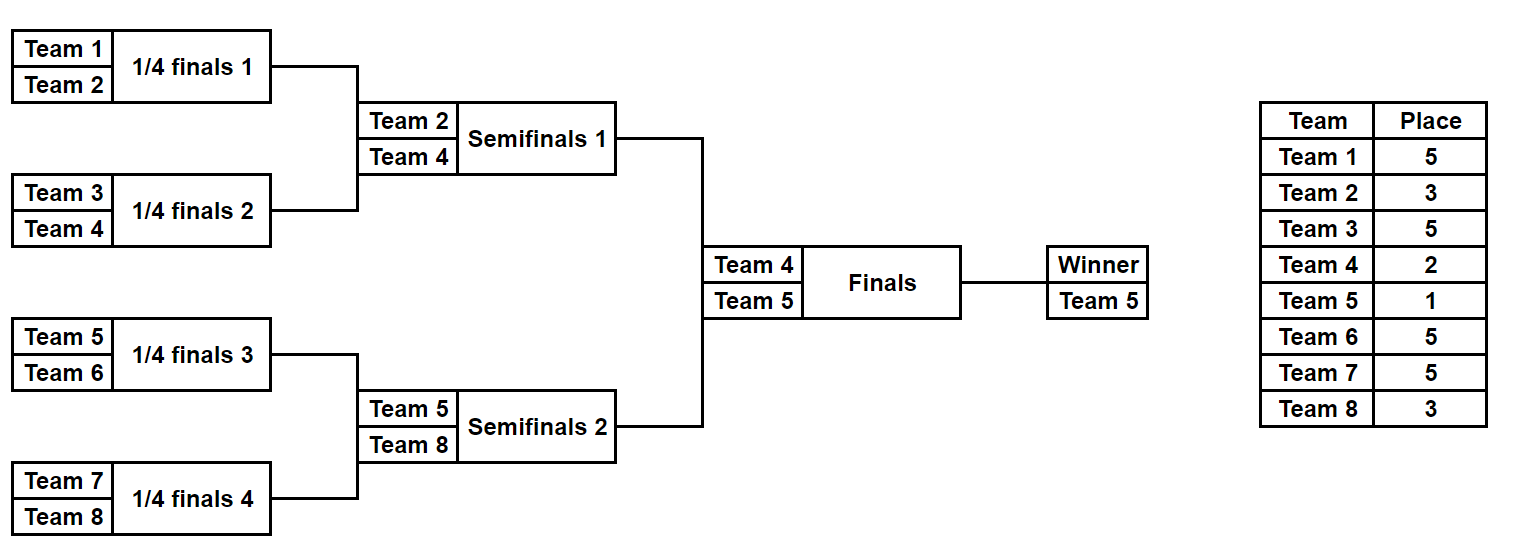 例如，下图描述了 $k=3$ 时比赛可能的一种过程以及各队伍的最终名次：  比赛结束后，结果被如下方式编码。令 $p_i$ 表示第 $i$ 支队伍的名次。比赛的哈希值 $h$ 计算方式为 $h = (\sum \limits_{i=1}^{2^k} i \cdot A^{p_i}) \bmod 998244353$，其中 $A$ 是给定的整数。 不幸的是，由于系统崩溃，几乎所有与比赛相关的数据都丢失了。仅剩下 $k$、$A$ 和 $h$ 的值。请你恢复各队伍的最终名次（如果可能）。

一行，包含三个整数 $k$、$A$ 和 $h$（$1 \le k \le 5$；$100 \le A \le 10^8$；$0 \le h \le 998244352$）。

如果不存在任何一种队伍名次分配方式与给定数据一致，输出一个整数 $-1$。 否则，输出 $2^k$ 个整数，第 $i$ 个整数表示第 $i$ 支队伍的名次 $p_i$。你的答案应当与某种可能的比赛过程一致，并且初始比赛结构是固定的（例如，第 $1$ 队和第 $2$ 队在第一轮必定对阵）。如果有多种可能的分配方式，输出任意一种均可。

第一个样例的比赛过程已在题目描述中给出。 对于第三个样例，名次分配 $[1, 2, 3, 3]$（第 $1$ 队获得第 $1$ 名，第 $2$ 队获得第 $2$ 名，第 $3$ 队和第 $4$ 队获得第 $3$ 名）在 $A=100$ 时哈希值为 $7020100$，但实际上不存在这样的比赛过程，因为第 $1$ 队和第 $2$ 队在半决赛中对阵，不可能同时获得前两名。 由 ChatGPT 4.1 翻译