CF1572E Polygon

You are given a strictly convex polygon with $ n $ vertices. You will make $ k $ cuts that meet the following conditions: - each cut is a segment that connects two different nonadjacent vertices; - two cuts can intersect only at vertices of the polygon. Your task is to maximize the area of the smallest region that will be formed by the polygon and those $ k $ cuts.

The first line contains two integers $ n $ , $ k $ ( $ 3 \le n \le 200 $ , $ 0 \le k \le n-3 $ ). The following $ n $ lines describe vertices of the polygon in anticlockwise direction. The $ i $ -th line contains two integers $ x_i $ , $ y_i $ ( $ |x_i|, |y_i| \le 10^8 $ ) — the coordinates of the $ i $ -th vertex. It is guaranteed that the polygon is convex and that no two adjacent sides are parallel.

Print one integer: the maximum possible area of the smallest region after making $ k $ cuts multiplied by $ 2 $ .

In the first example, it's optimal to make cuts between the following pairs of vertices: - $ (-2, -4) $ and $ (4, 2) $ , - $ (-2, -4) $ and $ (1, 5) $ , - $ (-5, -1) $ and $ (1, 5) $ , - $ (-5, 0) $ and $ (0, 5) $ . 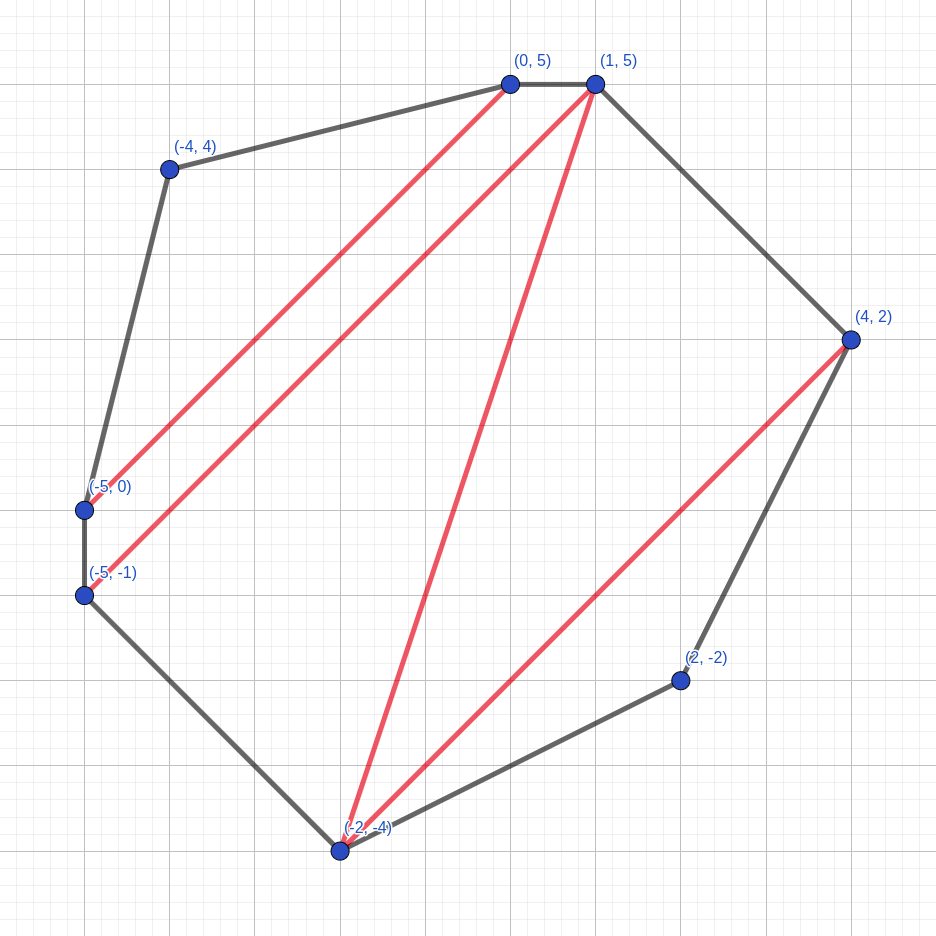 Points $ (-5, -1) $ , $ (1, 5) $ , $ (0, 5) $ , $ (-5, 0) $ determine the smallest region with double area of $ 11 $ . In the second example, it's optimal to make cuts between the following pairs of vertices: - $ (2, -1) $ and $ (0, 2) $ , - $ (2, -1) $ and $ (1, 0) $ , - $ (-1, 0) $ and $ (0, 2) $ . 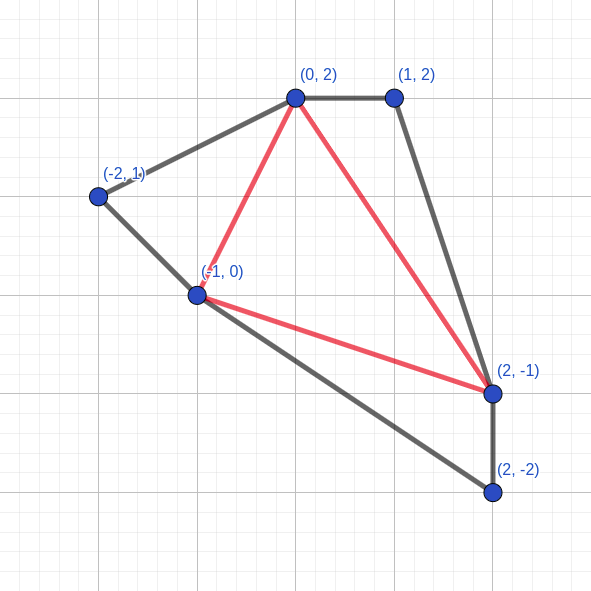 Points $ (2, -2) $ , $ (2, -1) $ , $ (-1, 0) $ determine one of the smallest regions with double area of $ 3 $ .