CF1575B Building an Amusement Park

Chanek 先生住在一个用平面表示的城市里。他想建造一个半径为 $r$ 的圆形游乐园。这个圆必须与原点（点 $(0, 0)$）相切。 城市中有 $n$ 个鸟类栖息地，可以作为游客在公园里的拍照点。第 $i$ 个鸟类栖息地位于点 $p_i = (x_i, y_i)$。 请你求出至少包含 $k$ 个鸟类栖息地的公园的最小半径 $r$。 当且仅当点 $p_i$ 到公园圆心的距离小于等于公园半径时，认为该点在公园内。注意，公园的圆心和半径不需要是整数。 本题保证给定的数据一定有解，且 $r \leq 2 \times 10^5$。

第一行包含两个整数 $n$ 和 $k$（$1 \leq n \leq 10^5$，$1 \leq k \leq n$），分别表示城市中鸟类栖息地的数量和公园内需要包含的鸟类栖息地数量。 接下来的 $n$ 行中，第 $i$ 行包含两个整数 $x_i$ 和 $y_i$（$0 \leq |x_i|, |y_i| \leq 10^5$），表示第 $i$ 个鸟类栖息地的位置。

输出一个实数 $r$，表示至少包含 $k$ 个鸟类栖息地的公园的最小半径。保证给定的数据一定有解，且 $r \leq 2 \times 10^5$。 如果你的答案的绝对误差或相对误差不超过 $10^{-4}$，则视为正确。 形式化地说，设你的答案为 $a$，标准答案为 $b$，当且仅当 $\frac{|a - b|}{\max{(1, |b|)}} \le 10^{-4}$ 时，你的答案被接受。

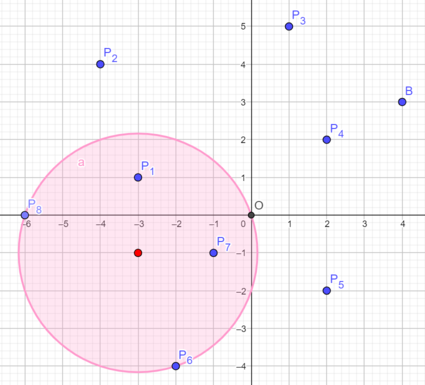
在第一个样例中，Chanek 先生可以将公园的圆心放在 $(-3, -1)$，半径为 $\sqrt{10} \approx 3.162$。可以证明这是最小的 $r$。 下图展示了第一个样例。蓝点表示鸟类栖息地，红色圆圈表示游乐园。  由 ChatGPT 4.1 翻译