CF1575J Jeopardy of Dropped Balls

Chanek 先生有一个新游戏，叫做“Dropping Balls”。一开始，Chanek 先生有一个大小为 $n \times m$ 的网格 $a$。 每个单元格 $(x, y)$ 包含一个整数 $a_{x, y}$，表示小球在该格的移动方向。 - $a_{x, y}=1$ —— 小球会向右移动（下一个格子为 $(x, y+1)$）； - $a_{x, y}=2$ —— 小球会向下移动（下一个格子为 $(x+1, y)$）； - $a_{x, y}=3$ —— 小球会向左移动（下一个格子为 $(x, y-1)$）。 每当一个小球离开某个格子 $(x, y)$ 时，该格子的整数 $a_{x, y}$ 会变为 $2$。Chanek 先生会依次投下 $k$ 个小球，每个小球都从第一行的第 $c_1, c_2, \dots, c_k$ 列（$1 \leq c_i \leq m$）开始下落。 请你确定每个小球最终会从哪一列离开网格（即小球离开网格时所在的列）。

第一行包含三个整数 $n$、$m$ 和 $k$（$1 \leq n, m \leq 1000$，$1 \leq k \leq 10^5$），分别表示网格的大小和小球的数量。 接下来的 $n$ 行，每行包含 $m$ 个整数 $a_{i,1}, a_{i,2}, \ldots, a_{i,m}$（$1 \leq a_{i,j} \leq 3$）。保证 $a_{i, 1} \ne 3$ 且 $a_{i, m} \ne 1$。 最后一行包含 $k$ 个整数 $c_1, c_2, \ldots, c_k$（$1 \leq c_i \leq m$），依次表示每个小球投下时所在的列。

输出 $k$ 个整数，第 $i$ 个整数表示第 $i$ 个小球最终离开网格时所在的列。

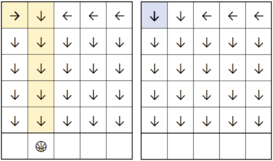
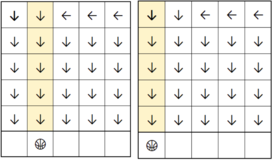
在第一个样例中，第一个小球的下落过程如下。注意，格子 $(1, 1)$ 的方向会变为向下。  第二个和第三个小球的下落过程如下。  所有小球都从第一行的第 $c_1, c_2, \dots, c_k$ 列依次投下。每个小球一旦离开网格就停止下落。 由 ChatGPT 4.1 翻译