CF1575M Managing Telephone Poles

Chanek 先生的城市可以表示为一个平面。他想在城市中建造一个住宅小区。 平面上有一些电线杆，用大小为 $ (n + 1) \times (m + 1) $ 的网格 $ a $ 表示。如果 $ a_{x, y} = 1 $，则在 $ (x, y) $ 处有一个电线杆。 对于每个点 $ (x, y) $，定义 $ S(x, y) $ 为该点到最近电线杆的欧几里得距离的平方。形式化地说，两个点 $ (x_1, y_1) $ 和 $ (x_2, y_2) $ 之间的欧几里得距离的平方为 $ (x_2 - x_1)^2 + (y_2 - y_1)^2 $。 为了优化建筑方案，项目主管要求你计算所有 $ S(x, y) $ 的和，其中 $ 0 \leq x \leq n $ 且 $ 0 \leq y \leq m $。请帮他求出 $ \sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} $ 的值。

第一行包含两个整数 $ n $ 和 $ m $（$ 0 \leq n, m < 2000 $），表示网格的大小。 接下来有 $ (n + 1) $ 行，每行包含 $ (m + 1) $ 个整数 $ a_{i, j} $（$ 0 \leq a_{i, j} \leq 1 $），表示平面上电线杆的位置。给定的网格中至少有一个电线杆。

输出一个整数，表示 $ \sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} $ 的值。

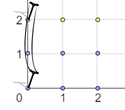
 在第一个样例中，点 $ (0,0) $、$ (1,0) $、$ (2,0) $、$ (0,1) $、$ (1,1) $ 和 $ (2,1) $ 最近的电线杆都在 $ (0, 0) $。而点 $ (0, 2) $、$ (1,2) $ 和 $ (2,2) $ 最近的电线杆在 $ (0, 2) $。因此，$ \sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} = (0 + 1 + 4) + (1 + 2 + 5) + (0 + 1 + 4) = 18 $。 由 ChatGPT 4.1 翻译