CF1575M Managing Telephone Poles

Mr. Chanek's city can be represented as a plane. He wants to build a housing complex in the city. There are some telephone poles on the plane, which is represented by a grid $ a $ of size $ (n + 1) \times (m + 1) $ . There is a telephone pole at $ (x, y) $ if $ a_{x, y} = 1 $ . For each point $ (x, y) $ , define $ S(x, y) $ as the square of the Euclidean distance between the nearest pole and $ (x, y) $ . Formally, the square of the Euclidean distance between two points $ (x_1, y_1) $ and $ (x_2, y_2) $ is $ (x_2 - x_1)^2 + (y_2 - y_1)^2 $ . To optimize the building plan, the project supervisor asks you the sum of all $ S(x, y) $ for each $ 0 \leq x \leq n $ and $ 0 \leq y \leq m $ . Help him by finding the value of $ \sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} $ .

The first line contains two integers $ n $ and $ m $ ( $ 0 \leq n, m < 2000 $ ) — the size of the grid. Then $ (n + 1) $ lines follow, each containing $ (m + 1) $ integers $ a_{i, j} $ ( $ 0 \leq a_{i, j} \leq 1 $ ) — the grid denoting the positions of telephone poles in the plane. There is at least one telephone pole in the given grid.

Output an integer denoting the value of $ \sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} $ .

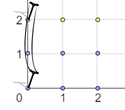In the first example, the nearest telephone pole for the points $ (0,0) $ , $ (1,0) $ , $ (2,0) $ , $ (0,1) $ , $ (1,1) $ , and $ (2,1) $ is at $ (0, 0) $ . While the nearest telephone pole for the points $ (0, 2) $ , $ (1,2) $ , and $ (2,2) $ is at $ (0, 2) $ . Thus, $ \sum_{x=0}^{n} {\sum_{y=0}^{m} {S(x, y)}} = (0 + 1 + 4) + (1 + 2 + 5) + (0 + 1 + 4) = 18 $ .