CF1576A Communication Routing Challenge

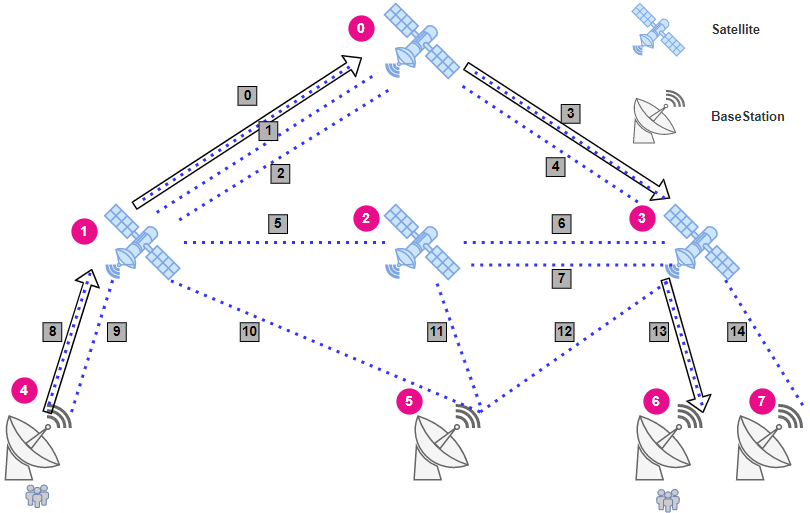
在光通信网络中，合理的路径规划可以提升通信资源的利用率，并为用户带来流畅的通信体验。下图展示了一个星间光通信网络。用户消息从一个地面基站（节点 $4$ 到 $7$）发出，通过空间中的卫星（节点 $0$ 到 $3$）传输，最终到达另一个地面基站（节点 $4$ 到 $7$）。  在上述图中，基站与卫星之间、卫星之间存在通信连接（简称边）。基站和卫星统称为节点。 用户消息在这些边上传输，称为流。有些用户可能与朋友进行视频通话，有些用户可能给家人发送短信，因此每个用户的消息流量（称为流速率）各不相同。 在两个节点之间存在多条平行边（例如边 $0$、$1$ 和 $2$），每条边的容量也不同。容量越大，能够传输的用户消息越多；传输距离越短，延迟越低，通信质量越好。 节点内部也有其结构。如图所示，节点内部的某些边之间无法互通，因为这些边（受限边对）并非完全连通。例如，节点 $2$ 内的边 $5$ 和边 $7$ 不能互通，因此流无法通过遍历这两条不连通的边经过节点 $2$。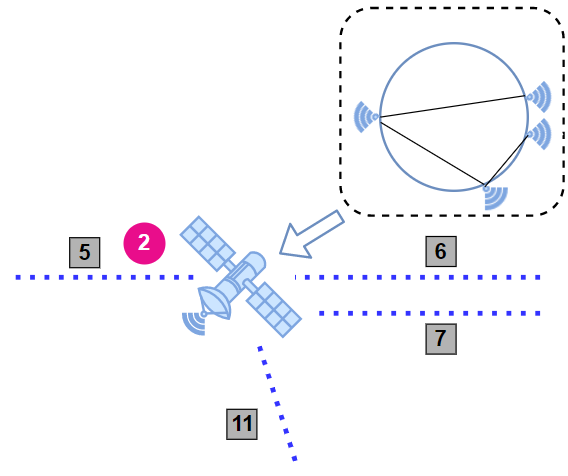  现在，输入网络中给定了每个用户流的源节点、目标节点和所需流速率。由于网络资源有限，可能无法为所有用户流成功计算路径。我们希望你能给出得分最高的方案。 注意： - 所有边都是无向的，因此流可以双向通过； - 边具有容量和长度（称为距离）； - 多个流可以共用同一条边； - 流可以同时以相反方向通过同一条边； - 在本题中，卫星与基站没有区别，因此流可以经过多个基站后到达目标基站。 约束条件 1. 每条边的容量有限。所有流在一条边上的总速率不能超过该边的容量。容量限制双向总流量。 2. 计算得到的流路径不允许有环或回路。 3. 由于卫星内部硬件限制，经过一个节点（包括源节点和目标节点）的流的数量不能超过该节点的站点流量上限（$ \mathit{SFL} $）。$ \mathit{SFL} $ 的值为 $200$。 4. 两节点之间存在多条平行边，这些边可能属于不同的组。每组内的链路由节点上的同一芯片管理，组内流量上限（$ \mathit{GFL} $）为 $100$。一组内所有边上的不同流的总数不能超过 $ \mathit{GFL} $。$ \mathit{GFL} $ 的值为 $100$。 5. 默认情况下，每个节点内所有边都是互通的。但存在一些受限边对——指定节点内的某些边对无法互通。 6. 每 $5$ 分钟内最多提交 $2$ 次。

第一行包含四个用空格分隔的整数：$ \mathit{NodeCount} $、$ \mathit{EdgeCount} $、$ \mathit{ConstrainedCount} $ 和 $ \mathit{FlowCount} $。 - $8 \leq \mathit{NodeCount} \leq 1400$， - $15 \leq \mathit{EdgeCount} \leq 15000$， - $3 \leq \mathit{ConstrainedCount} \leq 3600$， - $1 \leq \mathit{FlowCount} \leq 14000$。 接下来的 $ \mathit{EdgeCount} $ 行描述网络信息。每行包含六个整数：$ \mathit{EdgeID} $、$ \mathit{GroupID} $、$ \mathit{StartNodeID} $、$ \mathit{EndNodeID} $、$ \mathit{Distance} $ 和 $ \mathit{Capacity} $。 - $0 \leq \mathit{EdgeID} < \mathit{EdgeCount}$， - $0 \leq \mathit{GroupID} \leq 4500$， - $0 \leq \mathit{StartNodeID}, \mathit{EndNodeID} < \mathit{NodeCount}$， - $ \mathit{StartNodeID} \ne \mathit{EndNodeID} $， - $100 \leq \mathit{Distance} \leq 10000$， - $1 < \mathit{Capacity} \leq 10^5$。 保证只有多条边可能拥有相同的 $ \mathit{GroupID} $。 接下来的 $ \mathit{ConstrainedCount} $ 行描述网络中指定节点内无法互通的边对信息。每行包含三个整数：$ \mathit{NodeID} $、$ \mathit{EdgeID}_1 $ 和 $ \mathit{EdgeID}_2 $。 - $0 \leq \mathit{NodeID} < \mathit{NodeCount}$， - $0 \leq \mathit{EdgeID}_1, \mathit{EdgeID}_2 < \mathit{EdgeCount}$， - $ \mathit{EdgeID}_1 \ne \mathit{EdgeID}_2 $。 接下来的 $ \mathit{FlowCount} $ 行描述待计算的流信息。每行包含四个整数：$ \mathit{FlowID} $、$ \mathit{SourceNode} $、$ \mathit{TargetNode} $ 和 $ \mathit{FlowRate} $。 - $0 \leq \mathit{FlowID} < \mathit{FlowCount}$， - $0 \leq \mathit{SourceNode}, \mathit{TargetNode} < \mathit{NodeCount}$， - $ \mathit{SourceNode} \ne \mathit{TargetNode} $， - $2 \leq \mathit{FlowRate} \leq 12000$ 不要忘记，$ \mathit{SFL} $ 和 $ \mathit{GFL} $ 也是重要参数。 为简化起见，第 $i$ 条（$0$ 起始）边（流）的 $ \mathit{EdgeID} $ 和 $ \mathit{FlowID} $ 总是等于 $i$。

第一行输出你成功规划的流的数量。 接下来，每行输出一个流经过的路径的边信息。 格式如下：$ \mathit{FlowID}\ \mathit{EdgeID}_1\ \mathit{EdgeID}_2\ \mathit{EdgeID}_3\ \dots\ \mathit{EdgeID}_n $。 流路径之间的输出顺序不限，但同一流内的边必须按顺序输出，从源节点到目标节点。请输出所有成功计算路径的流。未输出的流，评测器默认你未找到合适路径。 评分规则 1. 违反约束、超时或超内存的解无效。 2. 按照公式 $ \mathit{Score} = \mathit{SuccessFlowNum} + \max \left(1 - \left(\frac{\mathit{AvgDistance}}{1000000}\right), 0\right) $ 评分（即成功规划流路径数越多得分越高；若成功流数相同，则平均路径距离越小得分越高。输出 $0$ 条流路径视为错误）。 3. 若得分相同，先提交者胜出。 4. 多组测试按总分排名。若某组无结果，则整体记为无结果。 5. 多次提交中得分最高者为最终得分。 6. 评测器仅在单核 CPU 上运行你的解，多线程实现不会带来收益。 7. 每 $5$ 分钟内最多提交 $2$ 次。

某一流路径的总距离为 $620$（$120 + 100 + 100 + 300 = 620$）。注意：$0\ 9\ 10\ 12\ 13$ 也是一个有效输出结果。 由 ChatGPT 4.1 翻译