CF1578D Dragon Curve

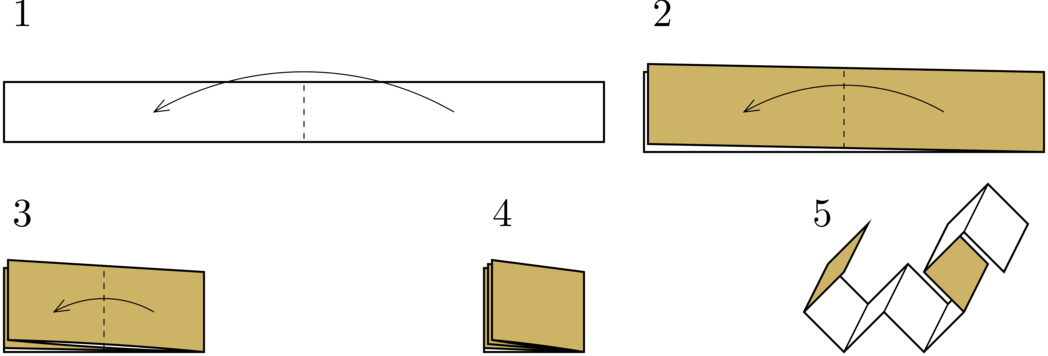
龙曲线是一种自相似的分形曲线。在本题中，龙曲线由若干长度相同、以直角连接的线段组成。构造龙曲线的一种简单方法如下：取一条纸带，连续 $n$ 次向同一方向对折，然后部分展开，使得各段以直角相连。如下图所示：  在这个例子中，构造了一个三阶龙曲线。一般来说，高阶龙曲线的前缀就是低阶龙曲线。因此，我们可以定义无限阶龙曲线，即有限阶龙曲线在阶数趋于无穷时的极限。 现在考虑四条无限阶龙曲线。它们都从原点（点 $(0,0)$）出发，每条线段的长度为 $\sqrt{2}$。四条曲线的第一段分别终止于 $(1,1)$、$(-1,1)$、$(-1,-1)$ 和 $(1,-1)$。每条曲线的第一次转弯都是向左（即，第一条曲线的第二段终止于 $(0,2)$）。在这种情况下，每一条线段都是一个以整数坐标为顶点的单位正方形的对角线，并且可以证明，每个这样的正方形恰好有一条线段经过。 给定一个点 $(x,y)$，你的任务是确定哪一条曲线上的哪一段线段经过了以 $(x,y)$ 和 $(x+1,y+1)$ 为对角顶点的正方形。曲线编号为 $1$ 到 $4$。曲线 $1$ 经过 $(1,1)$，曲线 $2$ 经过 $(-1,1)$，曲线 $3$ 经过 $(-1,-1)$，曲线 $4$ 经过 $(1,-1)$。线段编号从 $1$ 开始。

第一行包含一个整数 $n$（$1\le n\le2\times10^5$），表示测试用例的数量。 接下来的 $n$ 行，每行包含两个整数 $x$ 和 $y$（$-10^9\le x,y\le10^9$），表示坐标。

对于每个测试用例，输出一行，包含两个整数。第一个整数表示曲线的编号（$1$ 到 $4$ 之间的整数），第二个整数表示该曲线上线段的位置（第一段的位置为 $1$）。

你可以使用下图来调试你的解法：  由 ChatGPT 4.1 翻译